OMMEB 2017 ►
Presiona el título de cualquier problema para ver su página individual.
Nivel 1 Individual
Nivel 1 Equipos
Nivel 2 Individual
Nivel 2 Equipos
Nivel 3 Individual
Nivel 3 Equipos
• Regresar a la página de inicio
Nivel 1 Problema 1
Ricardo escribe una lista de números de acuerdo a la siguiente regla: a partir del tercer número de la lista, cada número es dos veces la suma de los dos números anteriores. El séptimo número de la lista es $8$, y el noveno es $24$. ¿Cuál es el onceavo número de la lista?
Nivel 1 Problema 2
Encuentre la cantitdad de múltiplos de $11$ en la sucesión:
\[99, 100, 101, 102,\dots,20130.\]
Nivel 1 Problema 3
Un granjero tiene $7$ vacas, $8$ ovejas y $6$ cabras. ¿Cuántas cabras más debe comprar para que la mitad de sus animales sean cabras?
Nivel 1 Problema 4
Los vértices $D$, $E$ y $F$ del rectángulo son los puntos medios de $\triangle ABC$. Si el área de $\triangle ABC$ es $48\text{cm}^2$, encuentra el área (en $\text{cm}^2$) del rectángulo $DEBF$.
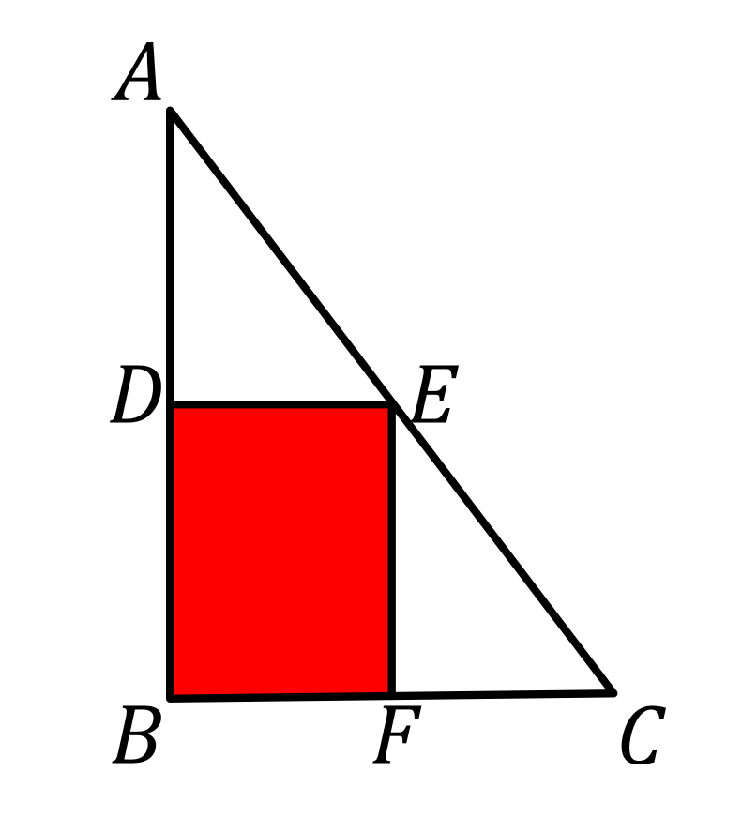
Nivel 1 Problema 5
Considera la siguiente sucesión de figuras. ¿Cuántos puntitos tendrá la figura $9$?
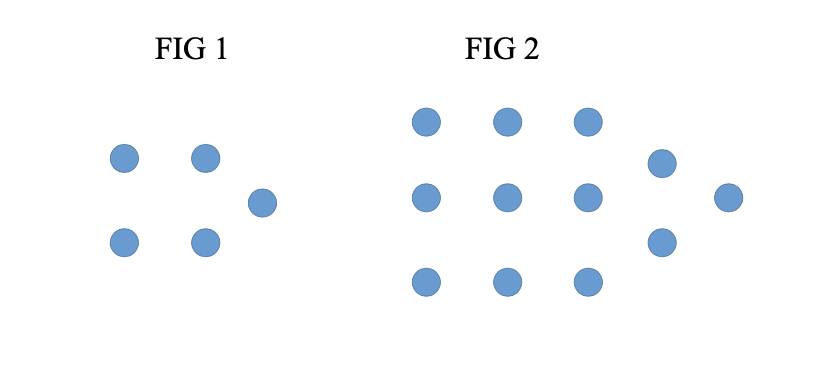
Nivel 1 Problema 6
Deeds le juega una broma a Hugo al esconderle la llave de su casa en una caja. Cuando Hugo llega al salón encuentra $4$ cajas: $3$ vacías y una que tiene la llave. Deeds dejó escrito el siguiente mensaje en la pizarra: “Exactamente una de las siguientes afirmaciones es verdadera:
- La llave está en la caja $3$ o la caja $4$
- La llave está en la caja $2$
- La llave no está en la caja $4$
- La llave está en la caja $1$ o en la caja $2$"
Nivel 1 Problema 7
En la siguiente figura, podemos ver 17 caras de los dados. Halla la suma de los números en las caras restantes.

Nivel 1 Problema 8
En $\triangle ABC$, $\angle ACB = 36^\circ$ y las bisectrices de los ángulos internos $\angle CAB$ y $\angle ABC$ se intersectan en $P$. Encuentre la medida en grados de $\angle APB$.
Nivel 1 Problema 9
El rectángulo $ABCD$ está dividido en cinco rectángulos congruentes como se muestra en la figura. Halla la razón $\frac{AB}{BC}$.
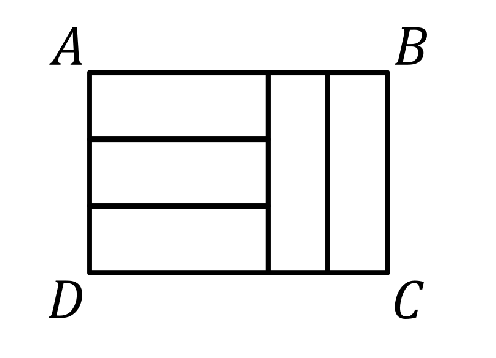
Nivel 1 Problema 10
Hay $100$ personas en una habitación. $60$ de ellos dicen que les gustan las matemáticas, pero solo a $50$ realmente les gustan. Por otro lado, $30$ niegan correctamente que les gustan las matemáticas, ¿cuántas personas les gustan las matemáticas pero se niegan a admitirlo?
Nivel 1 Problema 11
Drini y Deeds le dieron de propina a su mesero $50$ pesos cada quien. Drini le dio el equivalente a $4\%$ de su cuenta, mientras que Deeds le dio el equivalente $10\%$ de la suya. ¿Cuál es el suma total de ambas cuentas?
Nivel 1 Problema 12
El producto de los dígitos de un número de cuatro cifras es $810$. Si ninguno de los dígitos se repite, la suma de estos dígitos es:
Nivel 1 Problema 13
El diagrama de abajo muestra un pentágono (formado por la región $A$ y la región $B$) y un rectángulo (formado por la región $B$ y la región $C$) que se intersecan entre sí. La región de intersección $B$ es $3/16$ del pentágono y $2/9$ del rectángulo. Si la razón de la región $A$ del pentágono entre la región $C$ del rectángulo es $m/n$ es su forma simplificada, encuentre el valor de $m + n$.
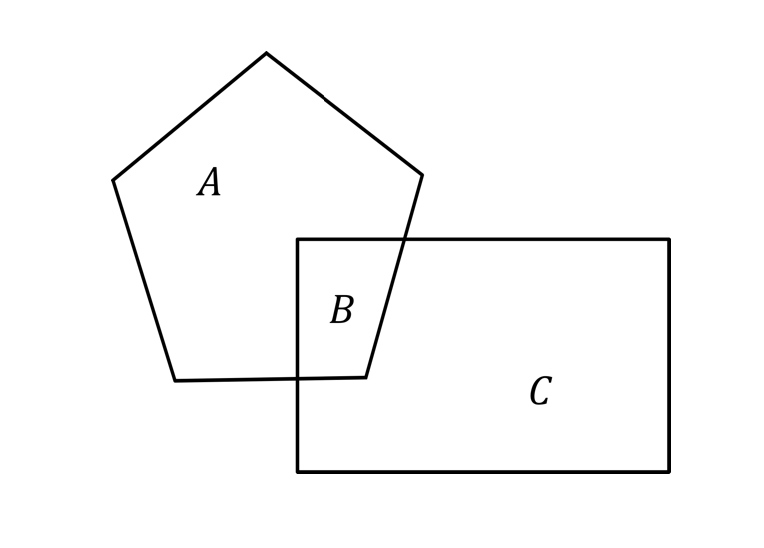
Nivel 1 Problema 14
Determina cuántos enteros positivos dividen a $5^8 + 2 \times 5^9$.
Nivel 1 Problema 15
El número de formas para acomodar $5$ niños y $6$ niñas en una fila de tal manera que las niñas puedan estar junto a otras niñas pero los niños no pueden estar junto a otros niños es $6! \times k$. Encuentre el valor de $k$.
Nivel 1 Equipos 1
El botón “$4$” de mi calculadora está estropeado, así que no puedo escribir números que contengan el dígito $4$. Más aún, mi calculadora tampoco muestra el dígito $4$ si $4$ es parte de la respuesta. Por esto no puedo escribir la cuenta $2 \times 14$. También, el resultado de multiplicar $3$ por $18$ se muestra como $5$ en vez de $54$ y el resultado de multiplicar $7 \times 7$ se muestra como $9$ en vez de $49$. Si multiplico un entero positivo de solo un dígito, por un positivo de dos dígitos en mi calculadora y ésta muestra $26$, ¿cuántas posibilidades pude haber multiplicado?
Nivel 1 Equipos 2
Sea $m=76^{2016}-76$. Halla el residuo cuando $m$ es dividido entre $100$.
Nivel 1 Equipos 3
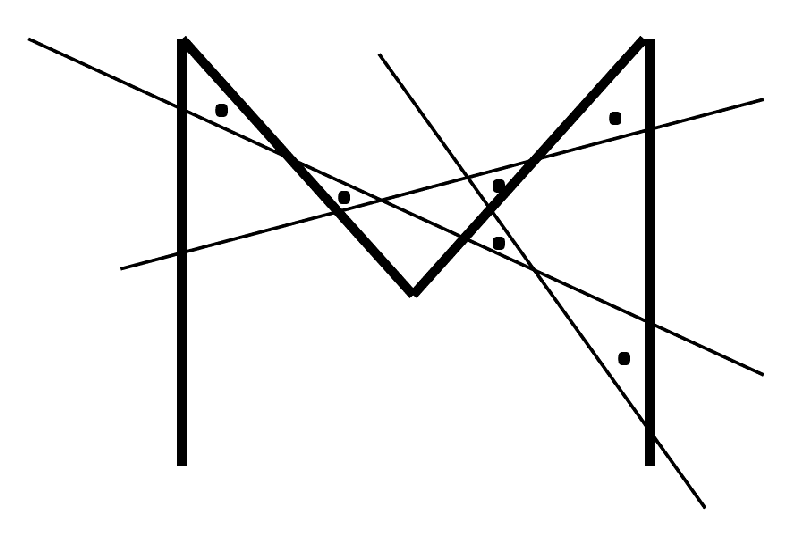
Deeds atraviesa la letra $M$ con tres rectas y obtiene exactamente $6$ triángulos, como lo indica la figura. Drini atraviesa la letra $M$ contres rectas y obtiene exactamente $9$ triángulos. Dibuja una posible manera que Drini pudo hacer esto.
Nivel 1 Equipos 4
Sean $p$ y $q$ dos primos consecutivos. Para algún entero fijo $n$, el conjunto $\{n-1,3n-19,38n-5,7n-45\}$ representa $\{p,2p,q,2q\}$, pero no necesariamente en ese orden. Encuentre el valor de $n$.
Nivel 1 Equipos 5
Ricardo tiene un jardín en forma de cuadrícula y en cada casilla una flor, como se muestra en la figura. Su esposa corta $12$ flores para poner en un florero y Ricardo observa que en cada renglón y columna de su jardín quedaron plantadas exactamente la misma cantidad de flores. Dibuja una de las posibles maneras en que la esposa de Ricardo pudo haber cortado las flores.

Nivel 1 Equipos 6
El conjunto $\{7,83,421,659\}$ tiene las siguientes propiedades:
- Todos sus elementos son números primos
- Al considerar todas las cifras que los conforman, aparecen todos los dígitos (excepto el $0$) exactamente una vez.
Nivel 1 Equipos 7
En la siguiente cuadrícula se escriben todos los números del $1$ al $9$ (sin repetir) de modo que la sumas de los tres números en cada renglón, columna o diagonal principal sea diferente. Luis ya puso el $1$ y el $5$ como se muestra en la figura. Termina de acomodar los restantes números.

Nivel 1 Equipos 8
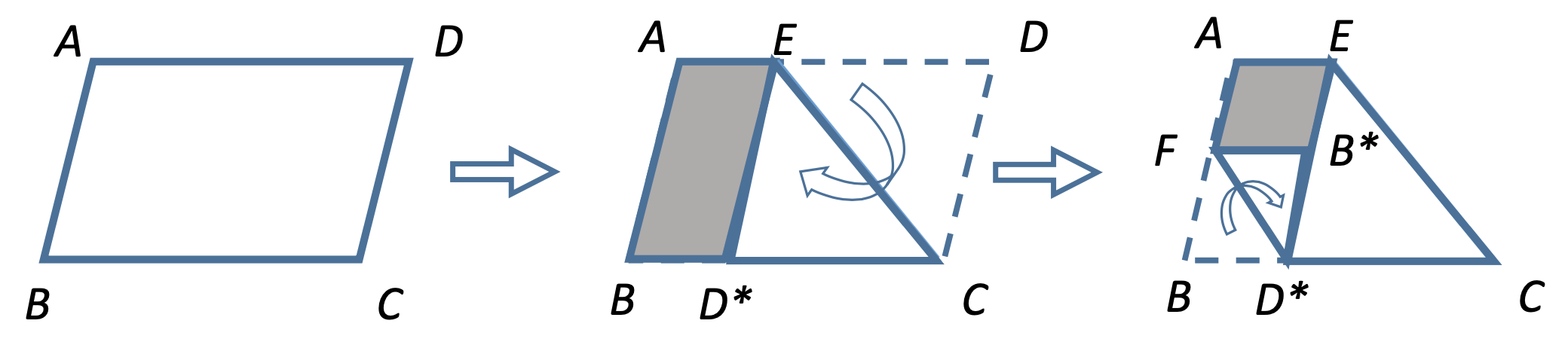
Un paraleogramo de papel se dobla desde la esquina superior derecha ($D$) como lo muestra la figura, de modo que la región sombreada tiene $3/8$ del área del paralelogramo original. A continuación, se vuelve a doblar sobre la esquina inferior izquierda ($B$) como lo muestra la figura. ¿A qué porción del área del paralelogramo original corresponde la región sombreada de la última figura?
Nivel 2 Problema 1
Los dígitos $2$, $2$, $3$, y $5$ se ordenan al azar para formar un número de cuatro dígitos. ¿Cuál es la probabilidad de que la suma del primer y el último dígito sea par?
Nivel 2 Problema 2
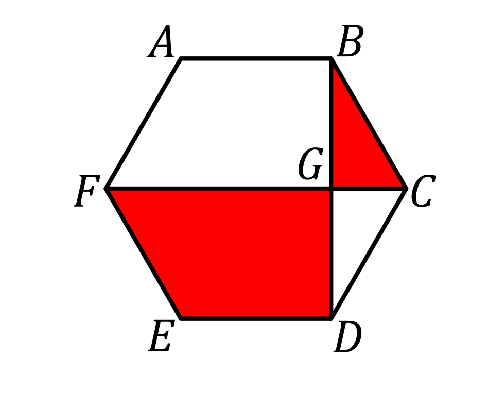
En el hexágono regular $ABCDEF$, dos de las diagonales, $FC$ y $BD$, se intersectan en $G$. La razón entre el área del cuadrilátero $FEDG$ y el área del $\triangle BCG$ es:
Nivel 2 Problema 3
Sesenta hombres trabajando en una construcción han hecho $1/3$ del trabajo en $18$ días. El proyecto está retrasado y debe ser completado en los siguientes doce días. ¿Cuántos trabajadores más se necesita contratar?
Nivel 2 Problema 4
Si todas las palabras que se pueden formar al permutar las letras de la palabra SMART son ordenadas alfabéticamente, ¿qué lugar ocupa la palabra SMART?
Nivel 2 Problema 5
En $\triangle ABC$ tenemos que $AB = AD$ y $\angle ABC − \angle ACB = 45^\circ$. Encuentra la medida en grados de $\angle CBD$.

Nivel 2 Problema 6
Juan calcula la suma de los primeros $n$ enteros positivos y encuentra que la suma es $5053$. Si ha contado un entero positivo dos veces, ¿cuál es este?
Nivel 2 Problema 7
¿Cuál es el mayor entero positivo $n$ que satisface $n^{200}\lt5^{300}$?
Nivel 2 Problema 8
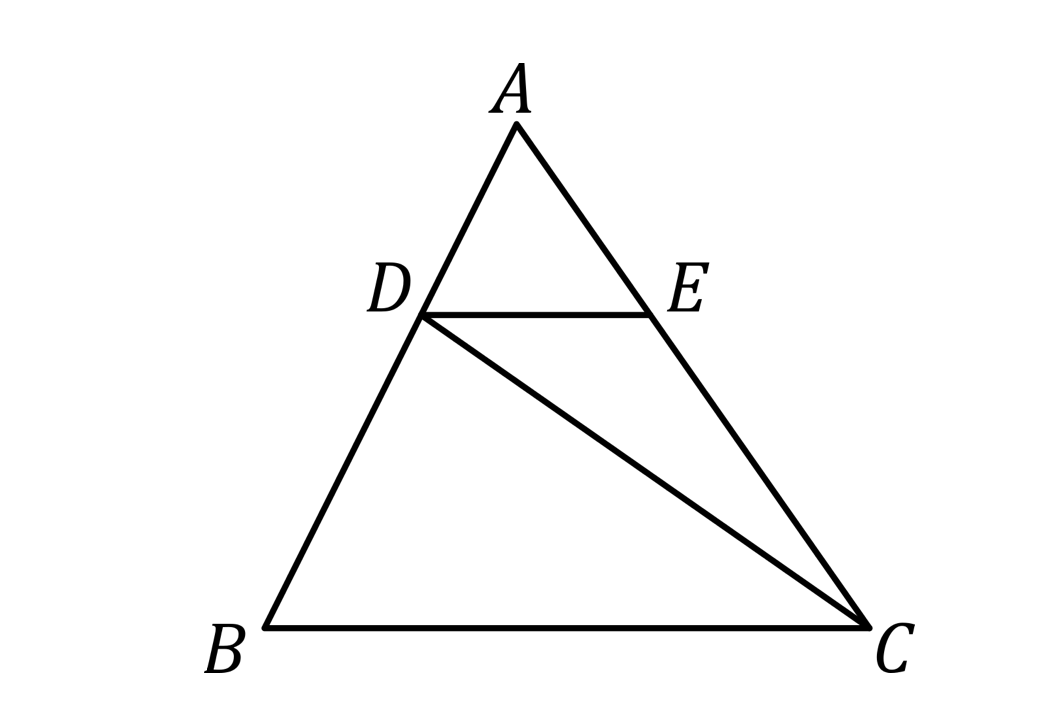
En la siguiente figura, si $DE\parallel BC$, Área $(\triangle ADE) = 1 \text{cm}^2$ y Área $(\triangle ADC) = 5 \text{cm}^2$, encuentre la medida en cm$^2$ de Área $(\triangle DBC)$.
Nivel 2 Problema 9
Si $a$ y $b$ son enteros positivos tales que $a^2+2ab-3b^2-41=0$, encuentre el valor de $a^2+b^2$.
Nivel 2 Problema 10
Encuentre el menor entero positivo $n$ tal que $2^8+2^{11}+2^n$ es un cuadrado perfecto.
Nivel 2 Problema 11
En la figura de abajo, se tiene que $BA = BC$, $AD = AF$, $EB = ED$. Halla la medida en grados de $\angle BED$.
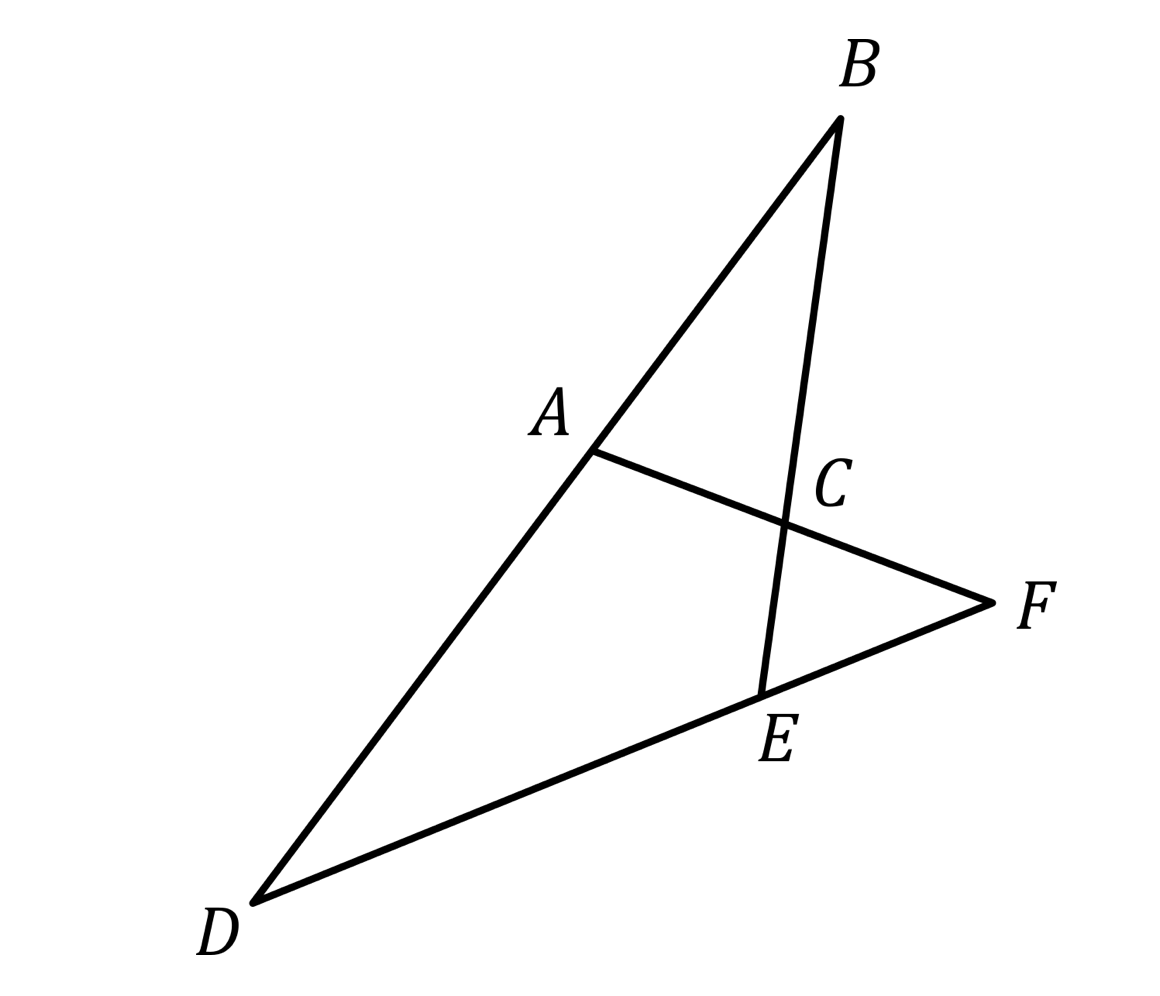
Nivel 2 Problema 12
Sean $a$, $b$, y $c$ números reales tales que $\frac{ab}{a+b}=\frac{1}{3}$, $\frac{bc}{b+c}=\frac{1}{4}$, $\frac{ca}{c+a}=\frac{1}{5}$. Encuentre el valor de \[\frac{24abc}{ab+bc+ca}.\]
Nivel 2 Problema 13
Sean $a$, $b$, $c$, $d$, $e$ enteros positivos que satisfacen $5a=4b=3c=2d=e$, y k=$a+2b+3c+4d+5e$. Encuentra el menor valor que puede tomar $k$.
Nivel 2 Problema 14
El diagrama de abajo muestra un rectángulo $ABLJ$, sonde el área de $ACD$, $BCEF$, $DEIJ$, y $FGH$ son $22$, $500$, $482$ y $22$, respectivamente. Encuentra el área de $HIK$.
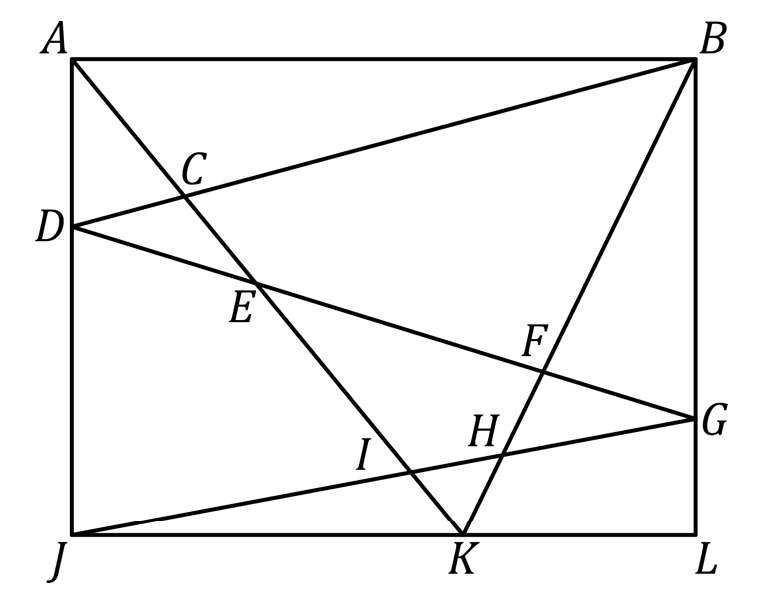
Nivel 2 Problema 15
¿Cuál es el mayor entero positivo $n$ para el cual $n^3+2006$ es divisible por $n+26$?
Nivel 2 Equipos 1
En una sala de fiestas, hay $9$ mesas ordenadas en una cuadrícula de $3\times 3$. Se tienen $3$ manteles verdes, $3$ blancos y $3$ rojos para poner sobre las mesas. ¿De cuántas maneras se pueden colocar los manteles de manera de que no hayan manteles del mismo color en cada renglón o columna?
Nivel 2 Equipos 2
Hugo le dice a Lalo: "Ya verifiqué en mi calculadora que solamente una de la ssiguientes parejas $(x,y)$ da como resultado un entero positivo al calcular $\sqrt{x^2+y^2}$." ¿Cuál es esa pareja?
- $x = 25530, y = 29464$;
- $x = 37615, y = 26855$;
- $x = 15123, y = 32477$;
- $x = 28326, y = 28614$;
- $x = 22536, y = 27462$.
Nivel 2 Equipos 3
Encuentra la parte entera de:
\[\frac{1}{\frac{1}{2010}+\frac{1}{2011}+\frac{1}{2012}+\frac{1}{2013}+\frac{1}{2014}+\frac{1}{2015}+\frac{1}{2016}}.\]
Nivel 2 Equipos 4
Sea $ABC$ un triángulo acutángulo con $BC \gt CA$. Sean $P$, $Q$ las intersecciones de la mediatriz del segmento $AB$ con las rectas $BC$ y $CA$, respectivamente. Sean $R$ el pie de la perpendicular desde $P$ a $CA$ y $S$ el pie de la perpendicular desde $Q$ a $BC$. Demuestra que $S$, $R$ y el punto medio de $AB$ son colineales.
Nivel 2 Equipos 5
El siguiente dibujo representa un mapa del juego buscaminas. En $10$ de los cuadritos hay una bomba. En los cuadritos marcados, los números indican cuántas bombas hay en los cuadritos junto a él (es decir, los cuadritos con los que comparte un lado o una esquina). Además, en los cuadritos marcados se sabe que no hay bombas. Indica en el diagrama con una $X$ la ubicación de los $10$ cuadritos que contienen bombas.
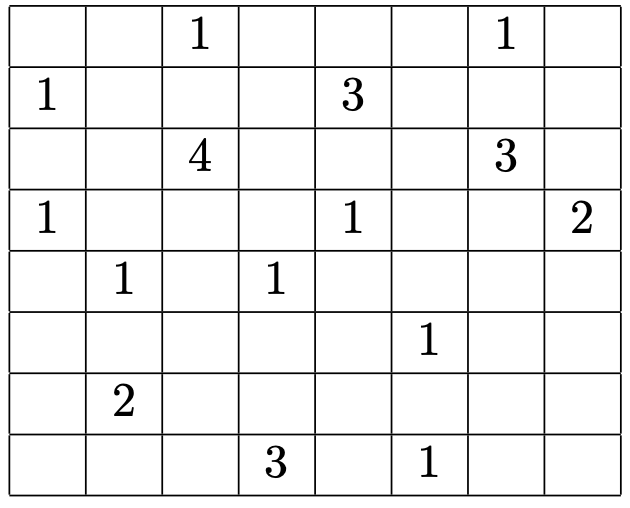
Nivel 2 Equipos 6
Halla el entero positivo más grande que divide a todos los números de la forma
\[(2n + 1)(2n + 3)(2n + 5)(2n + 7)(2n + 9),\]
donde $n$ es un entero positivo.
Nivel 2 Equipos 7
Dos grupos de olímpicos organizan un torneo de tenis, donde cada participante de cada uno de los grupos juega partidos contra todos los participantes del otro grupo. El día del torneo dos participantes estaban enfermos (uno de cada grupo), por lo que no pudieron asistir. Al final el número de partidos sin esos dos jugadores resultó $20\%$ menor que si hubieran asistido. Encuentra todos los posibles valores del número total de jugadores que participaron en el torneo.
Nivel 2 Equipos 8
Sea $p$ un número primo tal que $2p$ es la suma de los cuadrados de cuatro enteros consecutivos. Demuestra que $36$ divide a $p - 7$.
Nivel 3 Problema 1
Sea $N$ la suma de todos los múltiplos positivos de $8$ que no exceden $8000$. Halla el entero más cercano a $\sqrt{N}$.
Nivel 3 Problema 2
Halla el valor en grados de $a+b$ en el siguiente diagrama:
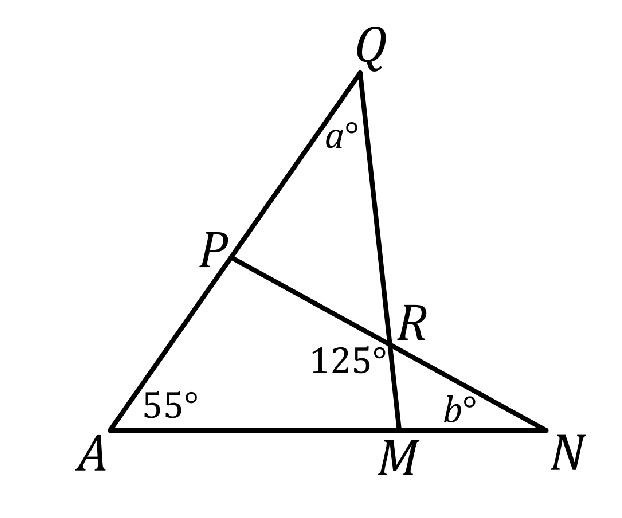
Nivel 3 Problema 3
Si $z^3-1=0$ y $z\neq 1$, encuentra el valor de $z + \frac1z + 4$.
Nivel 3 Problema 4
La edad de Lalo actualmente es el doble de la edad que tenía Jorge cuando Lalo tenía la edad actual de Jorge. Cuando Jorge tenga la edad que tiene Lalo, la suma de sus edades será $63$. Halla las edades actuales de Lalo y Jorge.
Nivel 3 Problema 5
$ABCD$ es un trapecio con $AB$ paralelo a $CD$. $E$ es el punto de intersección de $AC$ y $BD$. Si $AB=6$, $CD=15$, y el área de $\triangle ABC = 30$, ¿cuál es el área de $\triangle AEB$?
Nivel 3 Problema 6
Uge tira $6$ dados comunes. ¿Cuál es la probabilidad de que la suma sea $10$?
Nivel 3 Problema 7
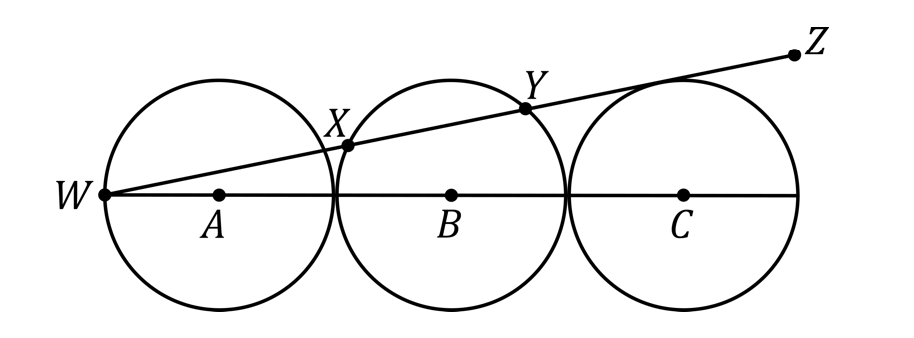
Tres círculos de radio $20$ son tangentes y sus respectivos centros $A$, $B$, y $C$, son colineales, como indica la figura. Si la linea $WZ$ es tangente al tercer círculo, encuentre la longitud de $XY$.
Nivel 3 Problema 8
Sean $m$, $n$ dos enteros positivos que satisfacen
\[\frac{1}{2\times3\times4} + \frac{1}{3\times4\times5} + \frac{1}{4\times5\times6} + \cdots + \frac{1}{13\times14\times15} + \frac{1}{14\times15\times16} =\frac mn.\]
Si $m/n$ es una fracción simplificada, halla el valor de $m+n$.
Nivel 3 Problema 9
Si $a+\frac{1}{a+1}=b+\frac{1}{b-1}-2$ y $a-b+2\neq 0$, halla el valor de $ab-a+b$.
Nivel 3 Problema 10
Sea $ABCDEF$ un hexágono tal que las diagonales $AD$, $BE$ y $CF$ se intersectan en el punto $O$, y el área de un triangulo formado por cualesquiera tres vértices consecutivos es $2$ (por ejemplo, Área $(\triangle BCD) = 2$). Encuentre el valor del área del hexágono.
Nivel 3 Problema 11
Hay cuatro pilas de piedras, una con $6$ piedras, dos con $8$, y una con $9$. Cinco jugadores numerados $1$, $2$, $3$, $4$ y $5$ toman turnos, en el orden de sus números, eligiendo una de las pilas y dividiéndola en dos pilas más pequeñas. El perdedor es el jugador que no pueda hacer esto. Di cuál es el número del jugador que pierde.
Nivel 3 Problema 12
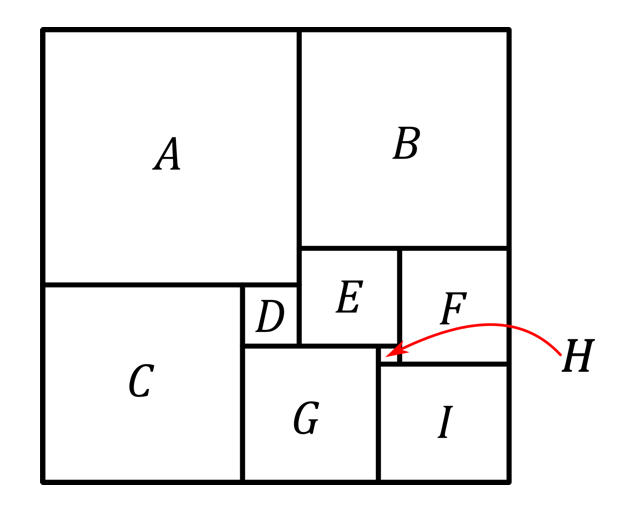
El siguiente rectángulo está formado por nueve piezas cuadradas de diferentes tamaños. Suponga que cada lado del cuadrado $E$ mide $7$. Halla el área del rectángulo.
Nivel 3 Problema 13
Sea $\nu(X)$ la suma de los elementos de un conjunto de números $X$. Calcula la suma de todos los números $\nu(X)$ donde $X$ es un subconjunto no vacío del conjunto $\{1, 2, 3, \dots, 16\}$.
Nivel 3 Problema 14
Un subconjunto $B$ de $A=\{1,2,3,\dots,2016\}$ se dice exacto si para cada $x\in B$ la suma de los elementos de $B-\{x\}$ tiene la misma cifra de las unidades que $x$.
- Demuestra que no existe ningún subconjunto exacto de $405$ elementos.
- Halla un subconjunto exacto de $400$ elementos.
Nivel 3 Problema 15
Si $\frac{a}{a^2+1}=\frac13$, determina el valor de
\[\frac{a^3}{a^6+a^5+a^4+a^3+a^2+a+1}.\]
Nivel 3 Equipos 1
Calcule $\sqrt[3]{77-20\sqrt{13}}+\sqrt[3]{77+20\sqrt{13}}$.
Nivel 3 Equipos 2
Si $\rvert x \lvert + x + 5y = 2$ y $\rvert y \lvert - y + x = 7$, encuentre el valor de $x+y+2016$.
Nivel 3 Equipos 3
Sea $n$ un número de $5$ cifras. Denotemos por $q$ y $r$ al cociente y residuo que se obtienen al dividir $n$ entre $100$. ¿Para cuántos valores de $n$ se tiene que $q + r$ es un múltiplo de $11$?
Nivel 3 Equipos 4
Uge olvidó la clave para desbloquear su teléfono, pero recuerda que tiene $5$ cifras distintas. Así que intentó con las siguientes claves: $40876$, $23497$, $15472$ y $75604$. En su primer intento exactamente dos números de su clave aparecen, pero en un lugar equivocado. En el segundo intento exactamente dos números coinciden con su clave. En el tercer intento exactamente un número coincide con su clave. En el cuarto intento exactamente un número de su clave aparece, pero en el lugar equivocado. Con esta información, ¿Puede Uge saber a ciencia cierta cuál es su clave? En caso afirmativo, escribe la clave de Uge. En caso negativo, explica por qué
Nivel 3 Equipos 5
Sobre una mesa se encuentran tres pelotas de radio $1$ y tangentes entre si. Sobre ellas se asienta una pelota de radio $2$. ¿A que altura sobre la mesa se halla el centro de la pelota grande?
Nivel 3 Equipos 6
Sean $a$ y $b$ enteros positivos con $a\gt b\gt 2$. Demuestre que $\frac{2^a+1}{2^b-1}$ nunca es un entero.
Nivel 3 Equipos 7
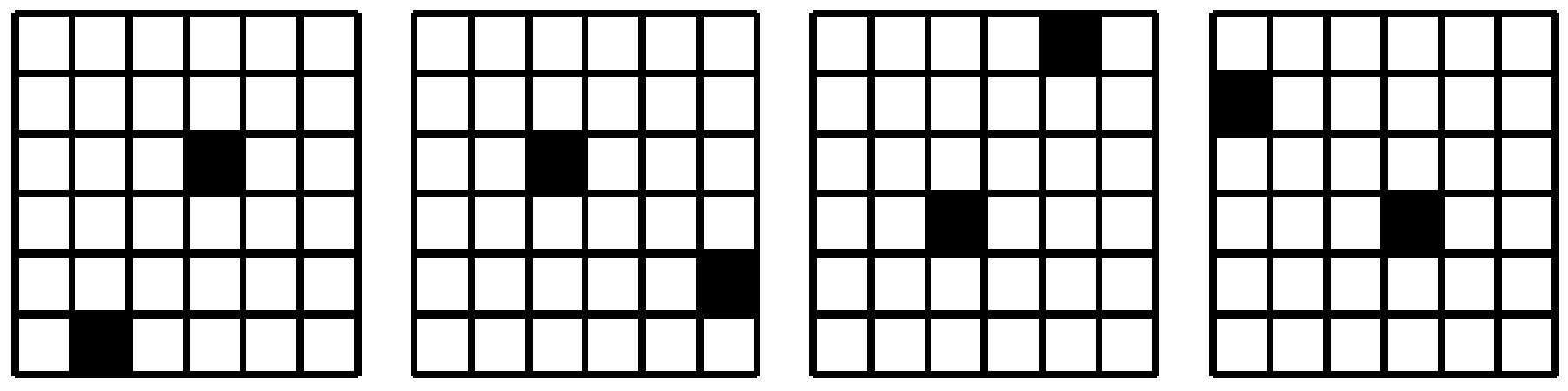
Deeds tiene un tablero blanco de $6 \times 6$ y desea pintarle dos casillas de negro. Dos coloraciones que difieran en una rotación se consideran equivalentes, por ejemplo, las cuatro coloraciones que se ilustran en la figura son todas equivalentes. ¿De cuántas maneras no equivalentes puede Deeds pintar su tablero?
Nivel 3 Equipos 8
Los puntos $K$ y $N$ se toman en los lados $AB$ y $AC$ de $\triangle ABC$, respectivamente, de manera que $KB = KN$. La bisectriz de $\angle ACB$ interseca al circuncírculo de $\triangle ABC$ en el punto $R$. La perpendicular de $R$ a la recta $AB$ interseca al segmento $BN$ en $D$. Demuestra que los puntos $A$, $K$, $D$, $N$ son concíclicos.