◄ OMMEB 2018 ►
Presiona el título de cualquier problema para ver su página individual.
Nivel 1 Individual
Nivel 1 Equipos
Nivel 2 Individual
Nivel 2 Equipos
Nivel 3 Individual
Nivel 3 Equipos
• Regresar a la página de inicio
Nivel 1 Problema 1
En cuatro días, seis máquinas impresoras han impreso $100$ libros. ¿Cuántos días tardarán en imprimir 50 libros si solo funcionan cuatro máquinas impresoras?
Nivel 1 Problema 2
La siguiente serpiente tiene $2018$ cuadritos que se han pintado de tres colores siguiendo el patrón: blanco, gris, negro, blanco, gris, negro, etc. ¿Cuántos cuadritos grises hay?
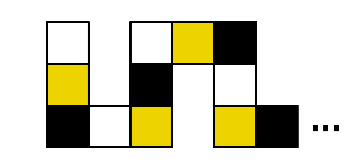
Nivel 1 Problema 3
A un club de matemáticas asisten $37$ estudiantes. Si las niñas se pueden dividir en equipos de $8$ sin que sobre ninguna y los niños se pueden dividir en equipos de $7$ niños sin que sobre ninguno, ¿cuántas niñas hay en el club?
Nivel 1 Problema 4
Decimos que un número natural es yucateco si tiene $9$ dígitos, todos son diferentes y ninguno de ellos es cero. ¿Cuál es la menor diferencia positiva posible entre dos números yucatecos?
Nivel 1 Problema 5
Mary tiene sus ahorros en un alcancía y decide gastarlos de la siguiente manera: El primer día gasta $20$ pesos, el segundo gasta $21$ pesos, el tercero $22$ pesos, el cuarto $23$ pesos y así sucesivamente de tal modo que cada día gasta un peso más que el día anterior. El día $18$ al ir a sacar sus monedas, se da cuenta que tiene en su alcancía exactamente un peso más que lo que gastó el día anterior, ¿cuánto tenía ahorrado Mary?
Nivel 1 Problema 6
Un entero positivo $n$ se dice que es maya si en la siguiente lista de números enteros consecutivos $101, 102, 103, \dots , 200$, hay exactamente un múltiplo de $n$. Encuentra el número maya más pequeño.
Nivel 1 Problema 7
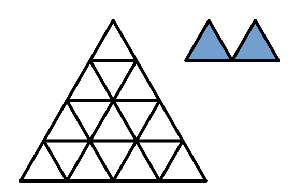
La siguiente figura se construyó con palillos de madera de la misma longitud. Si el perímetro del triángulo mayor es $96$ cm. ¿Cuál es la suma de las longitudes, en cm, de todos los palillos usados?

Nivel 1 Problema 8
La fracción $\frac 28$ es equivalente a $\frac 14$, y cuando agregas $1$ tanto al numerador como al denomidador de $\frac 28$ obtienes $\frac 39$, que es equivalente a $\frac 13$. Encuentra una fracción que sea equivalente a $\frac 18$, de manera que cuando agregues $1$ al numerador y al denominador de tu fracción, obtengas una fracción equivalente a $\frac 17$.
Nivel 1 Problema 9
Considera un trapecio $ABCD$, con los lados $BC$ y $DA$ paralelos y con $CD = DA = AB = \frac12 BC$, encuentra la medida en grados del ángulo $\angle CAB$.
Nivel 1 Problema 10
Si un triángulo equilátero y un hexágono regular tienen el mismo perímetro y el área del hexágono es de $120$ cm$^2$, ¿cuál es el área, en cm$^2$, del triángulo?
Nivel 1 Problema 11
En una pared está escrita la palabra YUCATAN con letras de metal. Al menos una de las letras se cayó, pero no se cayeron todas. ¿Cuántas palabras distintas pueden haber quedado escritas en la pared, sin considerar los espacios vacíos? Por ejemplo, si se cayerón la C y la T, queda YUAAN.
Nivel 1 Problema 12
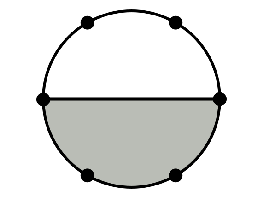
Un círculo se colorea de gris y blanco, y sobre la circunferencia están marcados $6$ puntos, como se indica en la figura. Decimos que un cuadrilátero es bicolor si su interior tiene una parte blanca y una parte gris. ¿Cuántos cuadriláteros bicolor tienen sus cuatro vértices en los puntos marcados?
Nivel 1 Problema 13
En un baile de la escuela, cada alumno bailó con $3$ alumnas y cada alumna bailó con $6$ alumnos. Si al baile asistieron $90$ personas entre alumnas y alumnos, ¿cuántos alumnos fueron al baile?
Nivel 1 Problema 14
Un rectángulo se divide en tres rectángulos más pequeños como se muestra en la figura. Cada uno de los rectángulos más pequeños cumple que sus lados están en la misma proporción que los lados del rectángulo grande. En cada uno de los cuatro rectángulos, ¿cuál es la razón de la longitud del lado más grande entre la longitud del lado más pequeño?

Nivel 1 Problema 15
Hugo escribe en su libreta exactamente una vez cada uno de los números de la forma $1\pm2\pm3\pm4\pm\dots\pm10$. Por ejemplo, uno de ellos es $1-2+3+4-5-6-7-8+9-10$. Encuentra la suma de todos estos números.
Nivel 1 Equipos 1
Ordena los siguientes números de menor a mayor:
\[3^6,4^5,5^4,6^3.\]
Nivel 1 Equipos 2
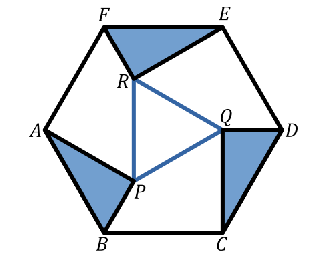
En un hexágono regular $ABCDEF$ de área $1$cm$^2$, se han trazado en su interior tres triángulos congruentes $ABP$, $CDQ$ y $EFR$ con ángulos de $30^\circ$, $60^\circ$ y $90^\circ$, los ángulos rectos en $P$, $Q$, $R$, como se muestra en la figura. Encuentra el área, en cm$^2$, del triángulo $PQR$.
Nivel 1 Equipos 3
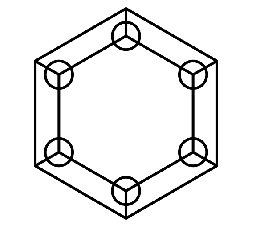
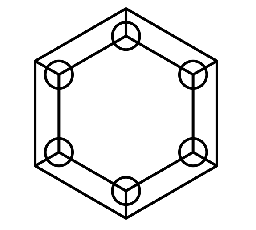
Se acomodan $7$ de los números del $1$ al $8$ en las caras de la siguiente figura, de forma que para cada tres caras que se toquen en un mismo círculo la suma de los números en tales caras sea un múltiplo de $3$. ¿Cuáles números podrían sobrar en estos tipo de acomodos?
Nivel 1 Equipos 4
Sergio y Zael quieren ir a una heladería a comprar un tipo de helado cada día de la semana. Dentro de los artículos que se venden se encuentran los siguientes: paletas, raspados y sándwich de nieve. Además, de cada uno de los artículos hay $4$ sabores: vainilla, fresa, chocolate y limón. Sergio quiere comprar un artículo de chocolate por día de manera que no coma lo mismo dos días seguidos, mientras que Zael quiere comprar paletas de distintos sabores sin comer dos días seguidos el mismo sabor. ¿Quién de los dos tiene más formas distintas de comprar a lo largo de toda la semana? Justifica tu respuesta.
Nivel 1 Equipos 5
Alguien cambió las etiquetas de los números de la calculadora de César. Los números deberían estar en la posición que muestra la imagen de la izquierda, pero sus posiciones fueron cambiadas a como se muestra en la imagen de la derecha. Como consecuencia de esto, cuando César aprieta el número $1$, la calculadora registra el número $3$ y al revés. Lo mismo pasa con el $4$ y con el $6$ y el $7$ y $9$. ¿Cuántas multiplicaciones distintas de dos números de un solo dígito, darán un resultado incorrecto cuando César utilice su calculadora? (Nota: las multiplicaciones $1 \times 2$ y $2 \times 1$ son consideradas multiplicaciones diferentes).

Nivel 1 Equipos 6
Encuentra el entero positivo más pequeño de seis dígitos, que cumpla que la suma de sus seis dígitos sea igual al producto de sus dígitos.
Nivel 1 Equipos 7
Acomoda ocho números enteros diferentes en los cuadritos que faltan, de manera que los productos de los tres números de cada renglón, de cada columna y de cada diagonal sean iguales.

Nivel 1 Equipos 8
Se quiere acomodar $8$ piezas como las de las derecha (las puedes rotar de ser necesario) de manera que se cubra toda la figura de la izquierda. ¿Cuántos acomodos diferentes se pueden hacer?
Nivel 2 Problema 1
¿Cuántos números primos dividen a $73^2 - 31^2 - 91$?
Nivel 2 Problema 2
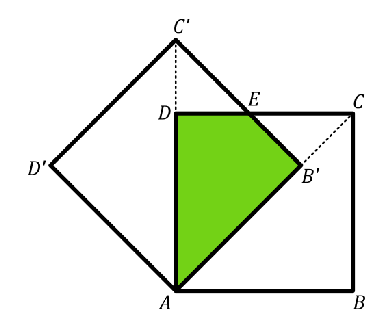
La siguiente figura se formó con dos cuadrados de lado $1$ cm, el $ABCD$ y el $AB'C'D'$, de manera que $AB'$ está sobre la diagonal $AC$. Sea $E$ el punto de intersección de $B'C'$ con $CD$. Encuentra el área, en cm$^2$ del cuadrilátero $AB'ED$.
Nivel 2 Problema 3
En un baile de la escuela, cada alumno bailó con $3$ alumnas y cada alumna bailó con $6$ alumnos. Si al baile asistieron $90$ personas entre alumnas y alumnos, ¿cuántos alumnos fueron al baile?
Nivel 2 Problema 4
Un rectángulo se divide en tres rectángulos más pequeños como se muestra en la figura. Cada uno de los rectángulos más pequeño cumple que sus lados están en la misma proporción que los lados del rectángulo grande. En cada uno de los cuatro rectángulos, ¿cuál es la razón de la longitud del lado más grande entre la longitud del lado más pequeño?

Nivel 2 Problema 5
Isaac y Alfredo juegan a lanzar dados de la siguiente manera. Isaac lanza un dado y apunta el número que salió en su libreta, luego vuelve a lanzar el dado y apunta el número que le salió a la derecha del número que ya había escrito, formando así un número de $2$ dígitos. Luego, Alfredo hace lo mismo que hizo Isaac. ¿Cuál es la probabilidad de que el número de Alfredo sea mayor que el número de Isaac?
Nivel 2 Problema 6
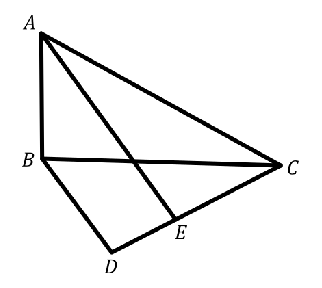
Sean $ABC$ un triángulo rectángulo con $\angle ABC = 90^\circ$, $D$ un punto que cumple que $BDC$ y $ABC$ son triángulos semejantes, además $A$ y $D$ están en lados opuestos de $BC$. El punto $E$ sobre $CD$ cumple que los ángulos $\angle CAE$ y $\angle EAB$ son iguales. Si $AE$ es paralelo a $BD$, ¿cuánto mide (en grados) el ángulo $\angle CAB$?
Nivel 2 Problema 7
Si un triángulo equilátero y un hexágono regular tienen el mismo perímetro y el área del hexágono es de $120$ cm$^2$, ¿cuál es el área, en cm$^2$, del triángulo?
Nivel 2 Problema 8
Sea ABCD un cuadrilátero tal que $AB=3$cm, $BC=4$cm, $CD=13$cm y $AD = 12$cm. Si $\angle ABC$ es recto, calcula el área, en cm$^2$, de $ABCD$.
Nivel 2 Problema 9
En una escuela hay $8$ alumnos que desean formar equipos de tres. ¿Cuántos equipos se pueden formar si se permite que dos equipos tengan a lo más un alumno en común?
Nivel 2 Problema 10
En una competencia internacional de matemáticas, el $28\%$ de los concursantes son de Asia, el $10\%$ de Oceanía. Los concursantes de África junto con los de Europa
son el $40\%$ del total, además Asia tiene $66$ alumnos más que los alumnos de África y entre alumnos de Europa y de Oceanía hay $187$ alumnos. ¿Cuántos concursantes europeos participaron?
Nivel 2 Problema 11
Sea $ABCD$ un rectángulo con diagonal $AC$, sea $Q$ un punto sobre $BC$ tal que $\angle BAQ = \angle QAD$ y $\angle QAC = 15^\circ$. Encuentra la medida en grados del ángulo $\angle BOQ$, donde $O$ es el punto medio de $AC$.
Nivel 2 Problema 12
Encuentra el mayor entero positivo $n$, tal que $n^2 + 2018n$ sea un cuadrado perfecto.
Nivel 2 Problema 13
Muestra que
\[\frac 43 + \frac 65 + \frac 87 + \cdots +\frac{102}{101}\]
no es un entero.
Nivel 2 Problema 14
En cada una de las $10$ regiones en que se ha dividido el círculo de la figura se colocan $3$ fichas. Un movimiento consiste en mover una ficha a una región vecina (es decir, a una región que comparte un radio). ¿Es posible que después de $2018$ movimientos todas las fichas se encuentren en la misma región? Justifica tu respuesta.

Nivel 2 Problema 15
Sea $ABCD$ un paralelogramo y sean $E$ un punto sobre $AB$ tal que los ángulos $\angle ADE$ y $\angle EDB$ son iguales, $F$ la intersección de $DE$ con $BC$ y $G$ la interseción de $AD$ con $CE$. Muestra que, $BC^2 = BF \cdot AG$.
Nivel 2 Equipos 1
Se acomodan $7$ de los números del $1$ al $8$ en las caras de la siguiente figura, de forma que para cada tres caras que se toquen en un mismo círculo la suma de los números en tales caras sea un múltiplo de $3$. ¿Cuáles números podrían sobrar en estos tipo de acomodos?
Nivel 2 Equipos 2
Encuentra el entero positivo más pequeño de seis dígitos, que cumpla que la suma de sus seis dígitos sea igual al producto de sus dígitos.
Nivel 2 Equipos 3
Encuentra todas las parejas de números reales $(x, y) $que cumplen las siguientes dos igualdades
\[x^3+y^3=1,\]
\[x^2+y^2=1.\]
Nivel 2 Equipos 4
Encuentra todas las parejas de enteros positivos $(a, r)$ tales que el número $N = a^2 +(a+r)^2 +(a+2r)^2 +(a+3r)^2 +(a+4r)^2$ tenga todos sus dígitos iguales.
Nivel 2 Equipos 5
Un triángulo $ABC$ con vértices sobre una circunferencia de centro $O$ tiene la siguiente propiedad: si $O$, $C'$ son simétricos con respecto a $C$ se cumple que \angle $CC'A = \angle ABC$. Encuentra el valor (en grados) del ángulo $\angle ABC$.
Nivel 2 Equipos 6
Se quiere acomodar $8$ piezas como las de las derecha (las puedes rotar de ser necesario) de manera que se cubra toda la figura de la izquierda. ¿Cuántos acomodos diferentes se pueden hacer?
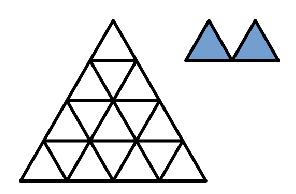
Nivel 2 Equipos 7
Los números creativos son números de $4$ dígitos $abcd$ tales que los números de dos dígitos $ab$, $cd$ son ambos pares. Además, la suma de sus dígitos es un número primo. Por ejemplo, $2018$ es número creativo, ya que $ab = 20$ y $cd = 18$ son números pares de dos dígitos y la suma $2 + 0 + 1 + 8 = 11$ es un número primo. ¿Cuántos números creativos menores o iguales al $2018$ hay?
Nivel 2 Equipos 8
Sea $ABCD$ un cuadrilátero. Muestra que si los cuatro triángulos $ABC$, $BCD$, $CDA$, $DAB$, tienen el mismo perímetro, entonces $ABCD$ es un rectángulo.
Nivel 3 Problema 1
Isaac y Alfredo juegan a lanzar dados de la siguiente manera. Isaac lanza un dado y apunta el número que salió en su libreta, luego vuelve a lanzar el dado y apunta el número que le salió a la derecha del número que ya había escrito, formando así un número de $2$ dígitos. Luego, Alfredo hace lo mismo que hizo Isaac. ¿Cuál es la probabilidad de que el número de Alfredo sea mayor que el número de Isaac?
Nivel 3 Problema 2
Sea ABCD un cuadrilátero tal que $AB=3$cm, $BC=4$cm, $CD=13$cm y $AD = 12$cm. Si $\angle ABC$ es recto, calcula el área, en cm$^2$, de $ABCD$.
Nivel 3 Problema 3
En una escuela hay $8$ alumnos que desean formar equipos de $3$. ¿Cuántos equipos se pueden formar, si se permite que dos equipos tengan a lo más un alumno en común?
Nivel 3 Problema 4
En una competencia internacional de matemáticas, el $28\%$ de los concursantes son de Asia, el $10\%$ de Oceanía. Los concursantes de África junto con los de Europa
son el $40\%$ del total, además Asia tiene $66$ alumnos más que los alumnos de África y entre alumnos de Europa y de Oceanía hay $187$ alumnos. ¿Cuántos concursantes europeos participaron?
Nivel 3 Problema 5
Sea $ABCD$ un rectángulo con diagonal $AC$, sea $Q$ un punto sobre $BC$ tal que $\angle BAQ = \angle QAD$ y $\angle QAC = 15^\circ$. Encuentra la medida en grados del ángulo $\angle BOQ$, donde $O$ es el punto medio de $AC$.
Nivel 3 Problema 6
Encuentra el mayor entero positivo $n$, tal que $n^2 + 2018n$ sea un cuadrado perfecto.
Nivel 3 Problema 7
La colección de números $a_n$ se define como sigue:
\[a_1=1\quad\text{y}\quad a_{n+1}=\frac{2a_n}{2+3a_n},\quad\text{para }n\geq 1.\]
Encuenta el valor numérico $a_{67}$
Nivel 3 Problema 8
Sea $ABC$ un triángulo isósceles cuyo ángulo en $A$ mide $24^\circ$, siendo éste el ángulo desigual. Un punto $D$ en la circunferencia de centro $C$ y radio $AC$ es tal que $BD$ interseca al segmento $AC$. La perpendicular a $BC$ por D corta a la circunferencia en E. Encuentra $\angle ADB + \angle BEA.$
Nivel 3 Problema 9
Lupita quiere invitarle un helado a cada uno de sus amigos Hugo, Ricardo y Deeds. Para ello tiene tres conos y $7$ bolas de helado para repartir: $2$ de chocolate, $2$ de vainilla, $2$ de fresa y $1$ de limón. ¿De cuántas maneras puede formar y repartir los helados, si usa las $7$ bolas y cada uno de sus amigos debe tener un número distinto (positivo) de bolas en su helado? Nota: Las bolas del mismo sabor son idénticas entre sí, pero el orden en que se distribuyen las bolas en un cono sí importa. Por ejemplo, los siguientes dos helados son distintos.
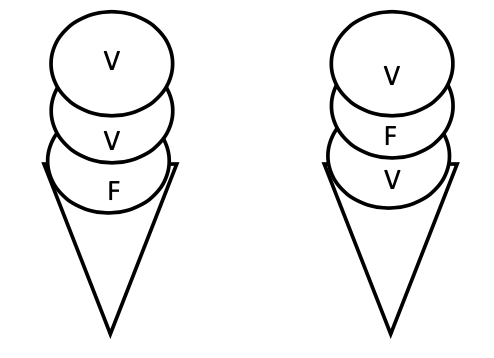
Nivel 3 Problema 10
Sea $P$ un polígono regular de $n$ lados y vértices $V_1, V_2, \dots , V_n$, y sea $O$ su centro. Determina todos los posibles valores de n para que la bisectriz de $\angle V_2V_1O$ pase por $V_3$.
Nivel 3 Problema 11
Una lancha cuando se desplaza en un río tranquilo va a $9$ $km/h$. Un día que había corriente en el río, José recorrió un kilómetro de ida y un kilómetro de regreso en $15$ minutos. ¿Cuál era la velocidad, en $km/h$, de la corriente del río ese día?
Nivel 3 Problema 12
En la siguiente figura, $ACDE$ es un rectángulo y se han dibujado la circunferencia inscrita al triángulo $AFE$ y su diámetro paralelo al lado $FE$. Encuentra la longitud, en cm, de $AB$.
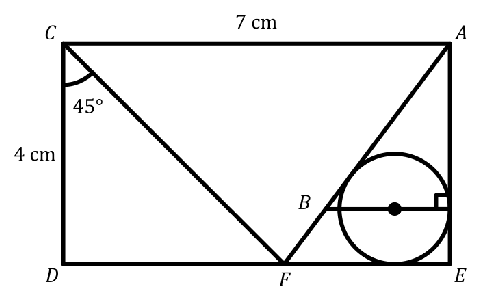
Nivel 3 Problema 13
En cada una de las $10$ regiones en que se ha dividido el círculo de la figura se colocan $3$ fichas. Un movimiento consiste en mover una ficha a una región vecina (es decir, a una región que comparte un radio). ¿Es posible que después de $2018$ movimientos todas las fichas se encuentren en la misma región? Justifica tu respuesta.

Nivel 3 Problema 14
Ana tiene cuatro hermanas: Berta, Ceci, Diana y Elena. Su edad actual es un número impar menor que $30$. Cuando Berta tenga el triple de la edad actual de Ana, se cumplirán las siguientes relaciones:
- La suma de las edades que tendrán en ese entonces Ana y Ceci será igual a la suma de las edades actuales de todas las hermanas.
- La edad de Diana será el triple de su edad actual.
- La edad de Elena será un año más que el doble de la edad actual de Berta.
Nivel 3 Problema 15
En la figura, el sector $AOB$ representa una cuarta parte de un círculo de radio $r = 1$ y el punto $C$ satisface que $\angle BOC = 45^\circ$. Sea $P$ un punto sobre el segmento $OB$ (distinto de $O$ y de $B$). Se trazan los segmentos $AP$ y $CP$ para formar la región sombreada. Demuestra que el área de la región sombreada es menor al área de la región sin sombrear.
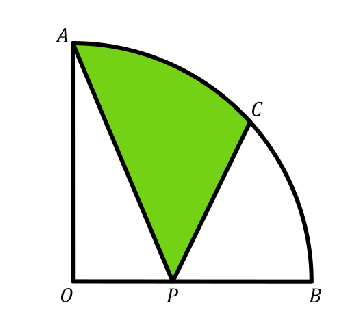
Nivel 3 Equipos 1
Sea $A = \{2, 5, 8, 11, \dots , 2018\}$, cada número, a partir del segundo, es el anterior más $3$. Determina el mínimo valor $k$ tal que si escogemos $k$ números del conjunto $A$, necesariamente hay dos distintos cuya suma sea $2020$.
Nivel 3 Equipos 2
Todos los números impares se dividen en grupos como se indica:
\[\{1\},\{3,5\},\{7,9,11\},\{13,15,17,19\},\dots\]
¿Cuál es la suma de los elementos del décimo grupo?
Nivel 3 Equipos 3
Un triángulo $ABC$ con vértices sobre una circunferencia de centro $O$ tiene la siguiente propiedad: si $O$, $C'$ son simétricos con respecto a $C$ se cumple que \angle $CC'A = \angle ABC$. Encuentra el valor (en grados) del ángulo $\angle ABC$.
Nivel 3 Equipos 4
Encuentra todas las parejas de enteros positivos $(a, r)$ tales que el número $N = a^2 +(a+r)^2 +(a+2r)^2 +(a+3r)^2 +(a+4r)^2$ tenga todos sus dígitos iguales.
Nivel 3 Equipos 5
Los números creativos son números de $4$ dígitos $abcd$ tales que los números de dos dígitos $ab$, $cd$ son ambos pares. Además, la suma de sus dígitos es un número primo. Por ejemplo, $2018$ es número creativo, ya que $ab = 20$ y $cd = 18$ son números pares de dos dígitos y la suma $2 + 0 + 1 + 8 = 11$ es un número primo. ¿Cuántos números creativos menores o iguales al $2018$ hay?
Nivel 3 Equipos 6
Sea $ABCD$ un cuadrilátero. Muestra que si los cuatro triángulos $ABC$, $BCD$, $CDA$, $DAB$, tienen el mismo perímetro, entonces $ABCD$ es un rectángulo.
Nivel 3 Equipos 7
Consideramos un tablero de $8 \times 8$. El Batab es una pieza que puede moverse de una casilla a otra vecina (que comparte un lado). Un camino del Mayab es un camino que va de una casilla inicial a una final tal que:
- Consta exclusivamente de movimientos del Batab.
- En cada paso se aleja del punto inicial y se acerca al punto final.
Nivel 3 Equipos 8
Los gemelos Adán y Beto van de su casa a la escuela. Adán, corre la mitad del trayecto y camina la otra mitad, mientras que Beto corre la mitad del tiempo y camina la otra mitad del tiempo. Los dos corren a una misma velocidad $v_1$ y los dos caminan a una misma velocidad $v_2.$ ¿Quién de ellos llega primero? Justifica tu respuesta.