◄ OMMEB 2019 ►
Presiona el título de cualquier problema para ver su página individual.
Nivel 1 Individual
Nivel 1 Equipos
Nivel 2 Individual
Nivel 2 Equipos
Nivel 3 Individual
Nivel 3 Equipos
• Regresar a la página de inicio
Nivel 1 Problema 1
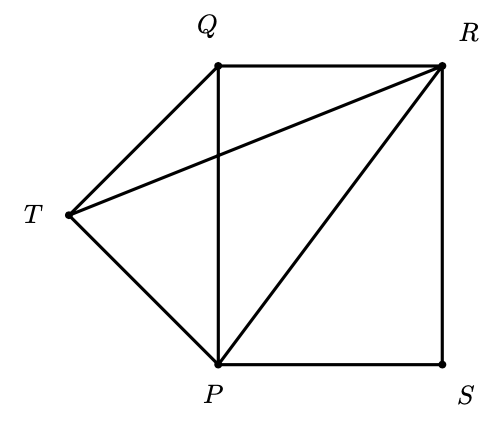
En la siguiente figura hay dos cuadrados unidos. ¿Cuántos triángulos rectángulos se pueden formar de manera que sus tres vértices sean puntos de $P,Q,R,S,T,U$?
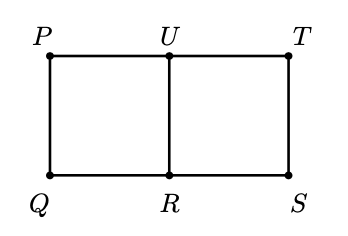
Nivel 1 Problema 2
El número $13$ es primo, y tiene la propiedad que al escribir sus dos dígitos (cifras) al revés se obtiene un número primo, en este caso el primo $31$. ¿Cuántos números primos de dos dígitos tienen esta propiedad?
Nivel 1 Problema 3
Encuentra el número capicuá más cercano a $2019$. Recuerda que un número capicuá es aquel que sus dígitos (cifras) se leen de la misma manera de izquierda a derecha que de derecha a izquierda, por ejemplo $1221$ y $212$ son capicuás.
Nivel 1 Problema 4
La figura de abajo es simétrica respecto a la recta punteada y se muestran algunas medidas sobre su contorno.
Si el perímetro de toda la figura es $50cm$, ¿cuál es, en $cm^2$, el área de la figura?
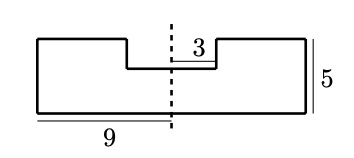
Nivel 1 Problema 5
¿Es posible pagar $\$25$ pesos con monedas de $\$1$ peso y monedas de $\$5$ pesos, usando exactamente $12$ monedas?
Nivel 1 Problema 6
Al número de tres dígitos (cifras) $4\square 7$ se le suma el número $321$ para dar como resultado el número de tres dígitos $7\triangle 8$. Si $7\triangle 8$ es divisible entre $9$, ¿cuánto vale la suma de $\square$ más $\triangle$?
Nota. Cada símbolo $\square$ y $\triangle$ representa un dígito.
Nivel 1 Problema 7
En un tablero de $3 \times 5$ cuadritos, ¿cuántos cuadrados se pueden dibujar de manera que sus vértices sean centros de los cuadritos de $1 \times 1$ del tablero?
Nivel 1 Problema 8
Luis tiene un nuevo restaurante, su amiga Laura le regaló mesas y sillas. Si las mesas las coloca de forma que cada una tenga $4$ sillas, le faltan $6$ sillas. Pero si colocan de dos en dos de forma que dos mesas juntas tengan $6$ sillas, le sobran $4$ sillas. ¿Cuántas mesas recibió Luis de regalo?
Nivel 1 Problema 9
En la figura se muestra un triángulo $ABC$ donde $\angle ABC = 120^\circ$. Además, se cumple que $AB = BC$, $A C = C D$, $A D = D E$, $A E = E F$ y que $\angle B C D = \angle C D E = \angle D E F = 1 5 0 ^\circ$. ¿Cuál es el valor, en grados, del ángulo $\angle EFA$?
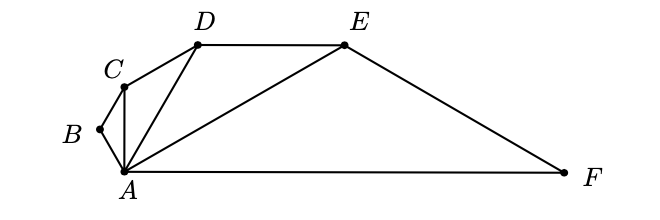
Nivel 1 Problema 10
Las caras de un dado tienen los números $1, 2, 3, 4, 5, 6$. Lalo forma números siguiendo tres pasos: Paso 1. Escoge tres caras y multiplica los tres números de estas caras; Paso 2. Encuentra el producto de los números de las otras tres caras; Paso 3. El número lo forma sumando los dos resultados anteriores. ¿Cuál es el número más pequeño que puede formar Lalo de esta manera?
Nivel 1 Problema 11
¿Cuántos números de dos dígitos (cifras) son iguales a la suma de sus dos dígitos más el producto de sus dos dígitos?
Nivel 1 Problema 12
Un número entero se llama ascendente si cada uno de sus dígitos (salvo el primero a la izquierda) es mayor que el dígito que está a su izquierda. Por ejemplo $2478$ es un número ascendente. ¿Cuántos números ascendentes hay entre $4000$ y $5000$?
Nivel 1 Problema 13
En la siguiente figura el triángulo $OPQ$ es isósceles con $OP = OQ$. La circunferencia de centro $O$ y radio $OQ$ corta a $OP$ en $B$, corta a $OQ$ en $C$ y toca a $PQ$ (tangentemente). El punto $A$ sobre la circunferencia cumple que $2AB = AC$. Si el área del $ABOC$ vale $2cm^2$, ¿cuál es el valor, en $cm^2$, del área del triángulo $OPQ$?
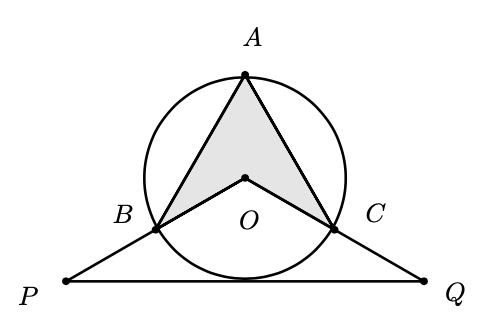
Nivel 1 Problema 14
(a) ¿Puedes escribir a $2048$ como suma de enteros consecutivos?
(b) ¿Puedes escribir a $2048$ como suma de enteros positivos consecutivos?
(b) ¿Puedes escribir a $2048$ como suma de enteros positivos consecutivos?
Nivel 1 Problema 15
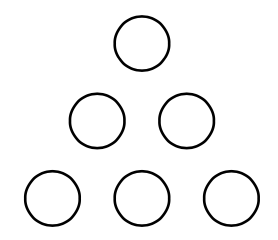
Lucy colocó los números $2, 3, 4, 5, 6$ y $10$ en los círculos de tal manera que el producto de los tres números de cada lado es el mismo, y cuidó que el producto fuera lo más grande posible. ¿Cuál es el valor de tal producto?
Nivel 1 Equipos 1
La suma rara (simbolizada con $\oplus$) es la suma normal más $1$, por ejemplo $2\oplus 3 = 2+3+1 = 6$, $1\oplus 0 = 1 + 0 + 1 = 2$. Encuentra el valor de:
\[1\oplus 0 \oplus 1 \oplus 0 \oplus \dots 1 \oplus 0,\]
en donde el $0$ se ha escrito $100$ veces.
Nivel 1 Equipos 2
¿De cuántas formas podemos cambiar un billete de $\$100$ pesos por monedas de $\$5$ pesos y de $\$2$ pesos, si tenemos que utilizar al menos una moneda de cada denominación?
Nivel 1 Equipos 3
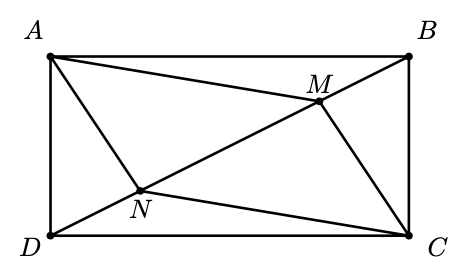
En un rectángulo $ABCD$ de área $40cm^2$, se construye el cuadrilátero $AMCN$ donde $M$ y $N$ son puntos en la diagonal $BD$ de manera que $BM = 3cm$, $MN = 4cm$ y $ND = 3cm$. ¿Cuál es, en $cm^2$, el área del cuadrilátero $AMCN$?
Nivel 1 Equipos 4
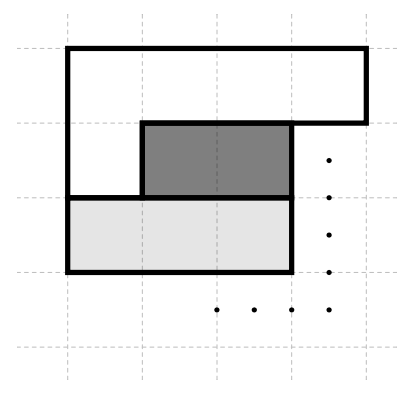
Marián comienza a pintar cuadritos siguiendo un patrón en espiral: pinta 2 negros, 3 grises, 5 blancos y luego repite pintando 2 negros, 3 grises, 5 blancos y así sucesivamente, tal como se observa en la figura. Marián deja de pintar cuando la figura sea un cuadrado. ¿Cuántos cuadritos pintó Marián?
Nivel 1 Equipos 5
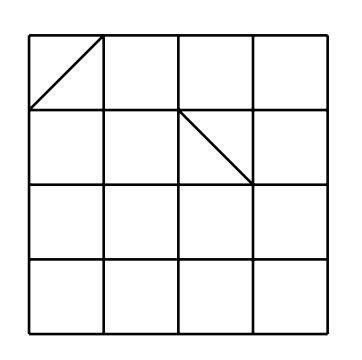
Considera un tablero de $4 \times 4$ con $16$ cuadritos. ¿Cuál es el mayor número de diagonales de cuadritos que se pueden dibujar, de manera que cualesquiera dos diagonales no tengan puntos comunes?
Nota. Por ejemplo se pueden dibujar diagonales como en la siguiente figura.
Nivel 1 Equipos 6
En el diagrama, $PQRS$ es un rectángulo. El punto $T$ está fuera del rectángulo y de manera que $PQT$ es un triángulo con $PT = QT$ y $\angle PTQ = 90^\cir$c. Si $PQ = 4cm$ y $QR = 3cm$, encuentra, en $cm^2$, el área del triángulo $PRT$.
Nivel 1 Equipos 7
Sobre cada una de las caras de un cubo se trazan las dos diagonales. Cada una de las aristas del cubo y cada una de las diagonales trazadas se quieren etiquetar con uno de los números $1$, $2$, $3$ de manera que todos los triángulos que se formen con tres de estos segmentos tengan las tres etiquetas en algún orden sobre sus lados. Da una manera de etiquetar.
Nivel 1 Equipos 8
Si $wxyz$ es un entero positivo de cuatro dígitos (cifras) con $w$ diferente de $0$, se llama la suma de capas de este entero a la suma $wxyz+xyz+yz+z$. Por ejemplo, la suma de capas del entero $4089$ es $4089+089+89+9=4276$.
- ¿Es posible que la suma de capas de algún entero $wxyz$ sea igual a $2019$?
- ¿Es posible que la suma de capas de algún entero $wxyz$ sea igual a $2020$?
Nivel 2 Problema 1
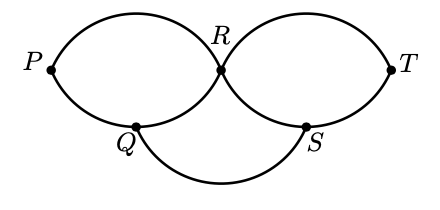
Cinco ciudades se comunican con un sistema de carreteras como se muestra en el dibujo. ¿Cuántos caminos diferentes puede seguir una persona que quiere ir de $P$ a $T$, siempre con dirección a la derecha?
Nivel 2 Problema 2
En una dulcería hay una máquina expendedora de dulces que tiene dos botones y un recipiente; después de insertar una moneda puedes apretar un solo botón, el botón $A$ deja caer $16$ dulces en el recipiente y el botón $B$ deja caer en el recipiente el $50\%$ de los dulces que hay en el recipiente. Si el recipiente al inicio esta vacío, ¿cuál es la mayor cantidad de dulces que se pueden obtener con $5$ monedas?
Nivel 2 Problema 3
Los vértices de un triángulo $ABC$ están en una circunferencia de manera que las medidas de los arcos $AB$, $BC$ y $CA$ son, respectivamente, $x + 75^\circ$, $2x + 50^\circ$ y $4x - 10^\circ$. Encuentra las medidas, en grados, de los ángulos internos del triángulo $ABC$.
Nota. El arco $AB$ es el que no contiene al vértice $C$, análogamente $BC$ y $CA$, no contienen a $A$ y $B$, respectivamente.
Nota. El arco $AB$ es el que no contiene al vértice $C$, análogamente $BC$ y $CA$, no contienen a $A$ y $B$, respectivamente.
Nivel 2 Problema 4
Benito compró comida para sus $4$ gatos, con la idea de que le alcanzará para $12$ días. En el camino se encontró otros dos gatos que los llevó a su casa. ¿Cuántos días le durará la comida ahora con los $6$ gatos?
Nivel 2 Problema 5
Encuentra la suma de los dos números capicuás más cercanos a $2019$. Recuerda que un número capicuá es aquel que sus dígitos (cifras) se leen de la misma manera de izquierda a derecha que de derecha a izquierda, por ejemplo $1221$ y $212$ son capicuás.
Nivel 2 Problema 6
Un padre y su hijo cumplen años el mismo día. En tres cumpleaños diferentes, la razón entre sus edades fueron $\frac 73$ , $\frac{13}{6}$ , $\frac 21$ . ¿Cuál es la diferencia de edades entre el padre y su hijo?
Nivel 2 Problema 7
Eugenio tiene $4$ borregos y una báscula que solo le permite pesar borregos en parejas (esto es, de dos en dos). ¿Cuál es la mínima cantidad de veces que Eugenio debe usar la báscula para conocer el peso de cada uno de sus borrego
Nivel 2 Problema 8
Cuatro amigos intercambian sus libros de olimpiada. Cada amigo tiene un libro para regalar a otro amigo, y recibirá un libro de un amigo diferente al que él regaló, (es decir, dos amigos no se intercambian libros). ¿De cuántas maneras se pueden intercambiar los libros?
Nivel 2 Problema 9
Sea $K$ una circunferencia con diámetro $AB$ y centro $O$. Sea $C$ un punto de $K$ tal que $\angle ABC = 60^\circ$. Sea $D$ un punto del arco $CA $(el de menor longitud) tal que $\angle AOD = 30^\circ$. Si $BC$ y $DO$ se intersecan en $P$, encuentra la razón del área del triángulo $ADO$ entre el área del triángulo $BPO$.
Nivel 2 Problema 10
Considera todos los números que se obtienen de $74477447$ al reordenar sus cifras, ¿cuántos de estos números son cuadrados perfectos?
Nivel 2 Problema 11
En una fiesta donde se baila en parejas chica-chico, se sabe que el $60\%$ de los chicos están bailando y el $80\%$ de las chicas están bailando. ¿Cuánta gente está bailando si en la fiesta hay exactamente $35$ personas?
Nivel 2 Problema 12
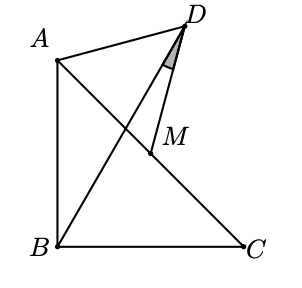
Sean $ABC$ un triángulo con $AB = BC$, $\angle ABC = 90^\circ$ y $M$ el punto medio de $AC$. Se construye el triángulo equilátero $ADM$ tal que $D$ y $B$ están en lados opuestos con respecto a $AC$. ¿Cuánto vale, en grados, el ángulo $\angle BDM$?
Nivel 2 Problema 13
En una bolsa hay $9$ canicas, de las cuales al menos una de ellas es verde. Además cuando sacas cualesquiera $4$ canicas hay al menos $2$ que son del mismo color; y cuando sacas cualesquiera $5$ de ellas hay a lo más $3$ del mismo color. ¿Cuántas canicas verdes hay en la bolsa?
Nivel 2 Problema 14
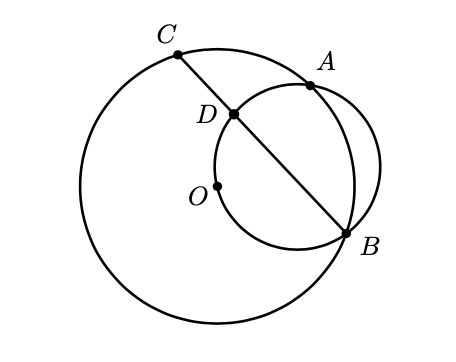
Sean $C_1$ una circunferencia con centro en $O$ y $C_2$ una circunferencia que pase por $O$ y corte a $C_1$ en $A$ y $B$. Sea $C$ un punto en $C_1$ ($O$ y $C$ del mismo lado respecto de la recta $AB$) y $D$ la intersección de $BC$ con $C_2$. Muestre que el triángulo $ADC$ es isósceles.
Nivel 2 Problema 15
Ana escoge $4$ números de entre $1, 2, 3, 4, 5, 6$. Si Ana le dijera a Beto cuál es el producto de los $4$ números que escogió, esta información no sería suficiente para que Beto pueda saber la paridad de la suma de los cuatro números escogidos por Ana. ¿Cuál es el producto de los cuatro números que eligió Ana?
Nivel 2 Equipos 1
Un entero positivo de cuatro dígitos es bidigital si su expresión decimal usa solamente dos dígitos y cada uno de ellos es usado dos veces. Por ejemplo, $2020$ es bidigital, mientras que $2222$ y $2111$ no lo son. ¿Cuántos números bidigitales hay?
Nivel 2 Equipos 2
Encuentra los enteros positivos $z$, para los cuales $\frac{5z + 64}{z+2}$ es una potencia de dos.
Nivel 2 Equipos 3
Un número es chido si la suma de sus dígitos entre el producto de sus dígitos, sin contar el $0$, es $2/3$. Ejemplo, $2019$ es chido porque la suma de sus dígitos es $2+1+9 = 12$ y el producto es $2\times 1\times 9 = 18$ y $\frac{12}{18} = \frac 23$. Encuentra el número chido más cercano a $2019$ (que sea distinto de $2019$).
Nivel 2 Equipos 4
¿De cuántas maneras diferentes se pueden colocar números de entre $0, 1, 2$, en cada uno de los cuadritos de un tablero de $5 \times 5$, de manera que cada subtablero de $2 \times 2$ cumpla que la suma de los cuatro números de sus cuadritos sea un múltiplo de $3$?
Nivel 2 Equipos 5
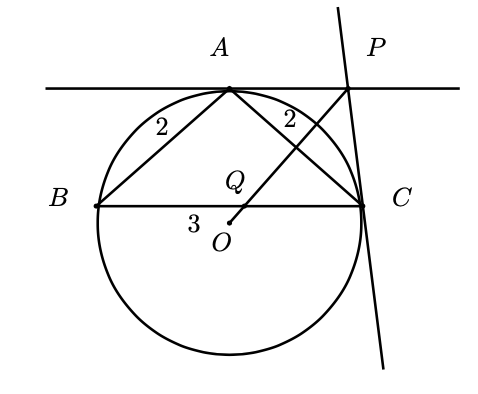
Sea $ABC$ un triángulo con $AB = AC = 2cm$ y $BC = 3cm$. Considera la circunferencia que pasa por los vértices $A,B,C$ y digamos que su centro es $O$. Se trazan las tangentes a dicha circunferencia que pasan por $A$ y por $C$, estas tangentes se cortan en $P$. El segmento $PO$ corta a $BC$ en $Q$. Calcula, en $cm$, la longitud de $CQ$.
Nivel 2 Equipos 6
¿Cuál es el menor entero positivo que no es divisor común de alguna pareja de enteros distintos de la lista $2,4,6,...,200$?
Nivel 2 Equipos 7
El primer término de una sucesión es $97$. Cada término subsecuente es la suma del dígito de las decenas y el cuadrado del dígito de las unidades del término anterior a él; por ejemplo, el segundo término es $9 + 72 = 58$. Encuentra el término $2019$ de tal sucesión.
Nivel 2 Equipos 8
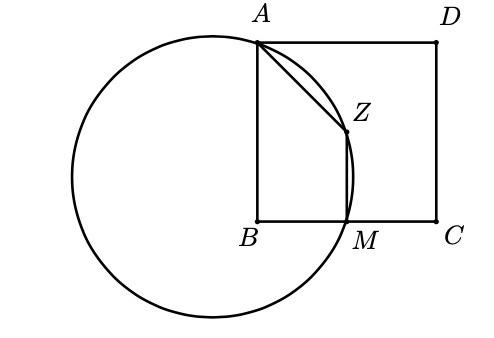
Sean $ABCD$ un cuadrado cuyo lado mide $2cm$, $M$ el punto medio del lado $BC$ y $Z$ el centro del cuadrado. Encuentra, en $cm$, el radio de la circunferencia que pasa por los puntos $A$, $M$ y $Z$.
Nivel 3 Problema 1
Las caras de un dado tienen los números $1, 2, 3, 4, 5, 6$. Lalo forma números siguiendo tres pasos: Paso 1. Escoge tres caras y multiplica los tres números de estas caras; Paso 2. Encuentra el producto de los números de las otras tres caras; Paso 3. El número lo forma sumando los dos resultados anteriores. ¿Cuál es el número más pequeño que puede formar Lalo de esta manera?
Nivel 3 Problema 2
Sea $ABCDE$ un pentágono regular cuyos vértices están en una misma circunferencia, sean $M$ y $N$ los puntos medios de los arcos $AB$ y $BC$. ¿Cuánto mide, en grados, el ángulo $\angle BMN$?
Nivel 3 Problema 3
En una bolsa tengo $2$ monedas de $\$1$, $3$ monedas de $\$5$, y $5$ monedas de $\$10$. Si saco $5$ monedas de la bolsa sin reemplazo (es decir, una vez que tomo una moneda la dejo afuera) y todas las monedas tienen la misma probabilidad de ser escogidas, ¿cuál es la probabilidad de sacar por lo menos $\$40$?
Nivel 3 Problema 4
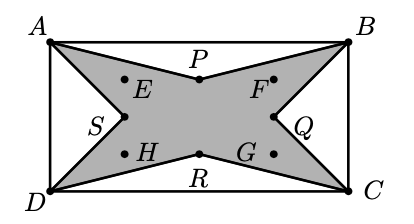
En un rectángulo $ABCD$ de área $40cm^2$, considera a $E$ y $G$, puntos en la diagonal $AC$ de manera que $AE = 2cm$, $EG = 6cm$ y $GC = 2cm$; considera también los puntos $F$ y $H$ en la diagonal $BD$, de manera que $BF = 2cm$, $FH = 6cm$ y $HD = 2cm$. Se construye una estrella de $4$ puntas $APBQCRDSA$, de manera que $P, Q, R, S$ son los puntos medios de los segmentos $EF, FG, GH y HE$, respectivamente. ¿Cuál es, en $cm^2$, el área de la estrella?
Nivel 3 Problema 5
En una fiesta donde se baila en parejas chica-chico, se sabe que el $60\%$ de los chicos están bailando y el $80\%$ de las chicas están bailando. ¿Cuánta gente está bailando si en la fiesta hay exactamente $35$ personas?
Nivel 3 Problema 6
Rogelio pinta los vértices de un cubo de $8$ colores distintos. ¿De cuántas formas se pueden acomodar las letras de la palabra OAXTEPEC en los vértices del cubo de tal manera que no haya $2$ letras E unidas por una arista?
Nivel 3 Problema 7
Considera todos los números que se obtienen de $74477447$ al reordenar sus cifras, ¿cuántos de estos números son cuadrados perfectos?
Nivel 3 Problema 8
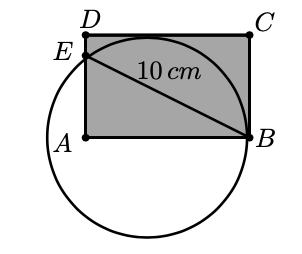
Encuentra, en $cm^2$, el área del rectángulo sombreado $ABCD$ de la siguiente figura, si se conoce que la longitud del segmento $BE$ es de $10 cm$, y la circunferencia es tangente a los lados $BC$ y $CD$ del rectángulo.
Nivel 3 Problema 9
¿Cuál es la menor cantidad de sumandos que se necesitan para escribir a $2019$ como suma de números que sean cuadrados perfectos?
Nivel 3 Problema 10
Para cada subconjunto de $\{1,2,3,4,5\}$, acomoda los números en orden decreciente (de mayor a menor) y realiza la suma con signos alternados; por ejemplo, si tomas al conjunto $\{5, 1, 2\}$ su suma alternada es $5 - 2 + 1 = 4$. ¿Cuánto vale la suma de todas las sumas alternadas cuando consideras todos los subconjuntos?
Nivel 3 Problema 11
Un padre y su hijo cumplen años el mismo día. En tres cumpleaños diferentes, la razón entre sus edades fueron $\frac 73$, $\frac{13}{6}$, $\frac 21$.. ¿Cuál es la diferencia de edades entre el padre y su hijo?
Nivel 3 Problema 12
Sean $f(x)$ y $g(x)$ dos polinomios de grado $2$ y $a,b,c,d$ números reales tales que $f(a) = 500$, $f(b) = 100$, $f(c) = 1000$, $f(d) = 2015$, $g(a) = 1519$, $g(b) = 1919$ y $g(c) = 1019$. ¿Cuánto vale $g(d)$?
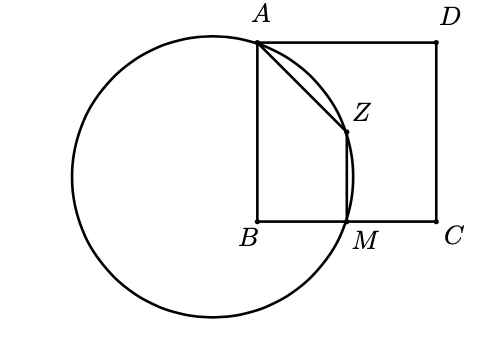
Nivel 3 Problema 13
Sean $ABCD$ un cuadrado cuyo lado mide $2 cm$, $M$ el punto medio del lado $BC$ y $Z$ el centro del cuadrado. Encuentra, en $cm$, el radio de la circunferencia que pasa por los puntos $A$, $M$ y $Z$.
Nivel 3 Problema 14
Un número natural es una quinta potencia si es de la forma $k^5$ para algún número natural $k$. Demuestra que si dos números naturales $n$, $m$ son tales que $n^2\cdot m^3$ es una quinta potencia entonces el número $n^3\cdot m^2$ también es una quinta potencia.
Nivel 3 Problema 15
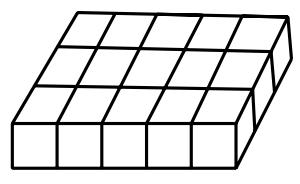
Hay $15$ cajas, acomodadas en un arreglo rectangular de $3 \times 5$, como se muestra en el siguiente dibujo, además en cada caja hay $7$ canicas. Una tirada consiste en elegir dos cajas que compartan un lado y sacar $2$ canicas, una de cada una de las dos cajas elegidas. ¿Cuál es el menor número de canicas que puede quedar, cuando ya no sea posible realizar una tirada?
Nivel 3 Equipos 1
Un triángulo acutángulo cumple que sus tres ángulos miden en grados un número entero y la medida del ángulo mayor es seis veces la medida del ángulo menor. Hallar las medidas, en grados, de los ángulos del triángulo.
Nivel 3 Equipos 2
El primer término de una sucesión es $97$. Cada término subsecuente es la suma del dígito de las decenas y el cuadrado del dígito de las unidades del término anterior a él; por ejemplo, el segundo término es $9 + 72 = 58$. Encuentra el término $2019$ de tal sucesión.
Nivel 3 Equipos 3
Carlos estaba jugando con los números y los acomodó de la siguiente manera. Empezó a formar caminos uniendo los números $1-2-3-4-5-6-7$ mediante segmentos de rectas horizontales o verticales en ese orden y tocando solo una vez cada número. Si continua así, ¿cuántos caminos pudo formar?

Nivel 3 Equipos 4
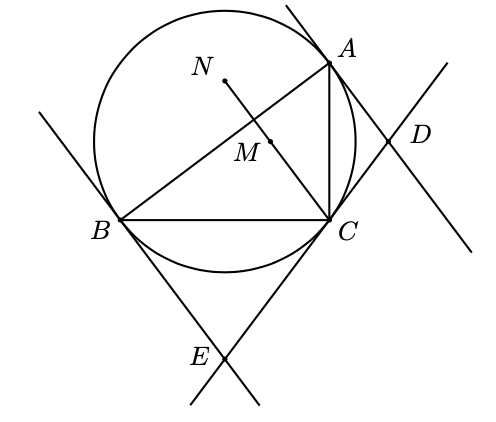
Sean ABC un triángulo con circuncírculo $\Gamma$, $\ell_1$, $\ell_2$, $\ell_3$ las tangentes a $\Gamma$ en $A$, $B$ y $C$ respectivamente. Denota por $D$ la intersección de $\ell_1$ y $\ell_3$ y por $E$ la intersección de $\ell_2$ y $\ell_3$. Sean $M$ el reflejado de $D$ con respecto a la recta $AC$ y $N$ el reflejado de $E$ con respecto a la recta $BC$. Muestra que si $M$, $N$ y $C$ están alineados, entonces $\angle ACB = 90^\circ$.
Nivel 3 Equipos 5
En una carrera de atletismo los corredores $A$, $B$ y $C$ fueron los primeros en llegar a la meta. Cuando $A$ llegó a la meta, los corredores $B$ y $C$ se encontraban a $2$ metros y a $2.98$ metros de $A$, respectivamente. Cuando llego $B$ a la meta el corredor $C$ estaba a $1$ metro de la meta. Suponga que cada una de las velocidades de los corredores son constantes durante la carrera. ¿De cuántos metros es la carrera?
Nivel 3 Equipos 6
Una tripleta Eliana consiste en tres números enteros positivos distintos que cumplen que la suma de dos de ellos es divisible entre el tercero de ellos. Encuentra el mayor valor que puede tener la suma de los elementos de una tripleta Eliana, teniendo la restricción de que el producto de sus elementos es a lo más $2019$.
Nivel 3 Equipos 7
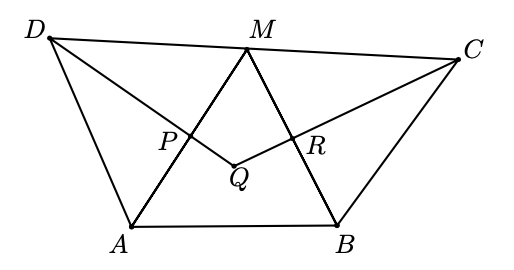
La figura $ABCD$ es un cuadrilátero. Las rectas $AM$, $BM$, $CQ$ y $DQ$ son bisectrices de los ángulos interiores en los vértices $A$, $B$, $C$ y $D$, respectivamente y de manera que $M$ se encuentre en $DC$. Sea $P$ la intersección de $AM$ con $DQ$ y sea $R$ la intersección de $BM$ con $CQ$. Si el cuadrilátero $PQRM$ es un rectángulo, encuentra el valor de la siguiente expresión:
\[\frac{AB+CD}{BC+DA}.\]
Nivel 3 Equipos 8
Muestra que no importa como se acomoden todos los números $1, 2, \dots , 25$ en los cuadritos de un tablero de $5 \times 5$, siempre hay un subtablero de $2 \times 2$ que satisface que los cuatro números de este subtablero suman más de $41$.