◄ OMMEB 2020 ►
Presiona el título de cualquier problema para ver su página individual.
Nivel 1 Individual
Nivel 1 Equipos
Nivel 2 Individual
Nivel 2 Equipos
Nivel 3 Individual
Nivel 3 Equipos
• Regresar a la página de inicio
Nivel 1 Problema 1
Nàm escribió un número en su cuaderno al cual multiplicó por $3$, al resultado le sumó $3$, después dividió entre $3$, por último restó 3. Si su resultado final fue $3$, ¿qué número escribió Nàm en su cuaderno?
Nivel 1 Problema 2
En cada cuadrito de la siguiente tabla se quiere escribir un número de entre $1$, $2$, $3$, $4$ y $5$, de tal manera que por un lado la suma de los números en cada renglón sea la misma, y por otro lado la suma de los números en cada columna sea la misma. Ya se escribieron algunos de los números. ¿Cuál es la suma de los $6$ números de los cuadritos?
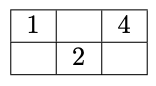
Nivel 1 Problema 3
Se va aplicar un examen en el auditorio de la escuela. El auditorio tiene $20$ filas de asientos, la primera fila tiene $10$ asientos y cada fila sucesiva tiene un asiento más que la fila anterior. Para hacer el examen los alumnos se deben sentar de manera que en cada fila de asientos entre cada dos alumnos deben quedar dos asientos vacíos. ¿Cuál es el máximo número de alumnos que pueden sentarse en el auditorio?
Nivel 1 Problema 4
Diana va a colorear los números enteros positivos con uno de los colores verde, blanco y rojo, siguiendo las siguientes indicaciones:
- La suma de dos números (que pueden ser iguales) pintados de verde, se pinta de rojo.
- La suma de dos números (que pueden ser iguales) pintados de rojo, se pinta de verde.
- La suma de dos números uno pintado de verde y otro pintado de rojo, se pinta de blanco. Si inicia pintando al número $1$ de rojo, ¿de qué color quedará pintado el número $2020$?
Nivel 1 Problema 5
Se quiere construir una alambrada en forma de cubo de dimensiones $4 cm \times 4 cm \times 4 cm$ de manera que la alambrada quede dividida en cubitos de $1 cm \times 1 cm \times 1 cm$ como se ve en la figura. ¿Cuántos centímetros de alambre se necesitan?
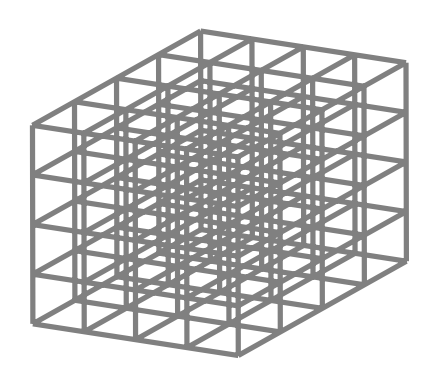
Nivel 1 Problema 6
Un pintor realizó un mural con puros cuadrados. El primer día pintó un cuadrado de $1m \times 1m$, el segundo día se pintó uno de $1m\times 1m$ y otro de $2m\times 2m$, el tercer día cuadrados de $1m\times 1m$, $2m\times 2m$ y de $3m\times 3m$ y así sucesivamente. Después de haber pintado $250$ metros cuadrados en total, el pintor se detuvo. ¿Qué cantidad de metros cuadrados pintó el último día el pintor?
Nivel 1 Problema 7
Se tienen tres cajas de las cuales una contiene dos bolas, cada una marcada con el número $1$; otra contiene dos bolas, cada una marcada con el número $2$, y la tercera contiene una bola marcada con el $1$ y una bola marcada con el $2$. Los contenidos están indicados con las etiquetas $11$, $22$ y $12$ que han sido equivocadamente pegadas en las cajas, de suerte que ninguna de las cajas lleva la etiqueta correcta. Para restituir a cada caja la etiqueta que le corresponde, se permite entreabrir una caja, solo el tiempo necesario para ver que número tiene una de las bolas. ¿Qué etiqueta tiene la caja que se debe destapar?
Nivel 1 Problema 8
En la siguiente figura hay un rectángulo que se ha dividido en triángulos. ¿Cuántos ángulos agudos hay en la figura?
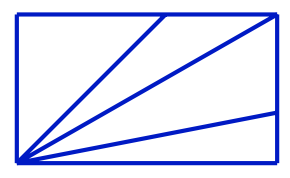
Nivel 1 Problema 9
Cada número de $3$ cifras decimales se divide entre la suma de sus $3$ cifras y da un resultado. Por ejemplo, el número $207$ se divide entre $2+0+7=9$ dando como resultado $\frac{207}{9}=23$. ¿Cuál es el mayor valor que se puede obtener como resultado, al considerar todos los números de tres cifras?
Nivel 1 Problema 10
Usando las siguientes fichas se pueden formar $325$ números diferentes, algunos números usan solamente una ficha, otros dos fichas y otros tres, cuatro o cinco fichas. ¿Cuántos de estos números no son múltiplos de $9$?

Nivel 1 Problema 11
¿Cuál es la razón del área de la figura de la izquierda entre el área de la figura de la derecha?
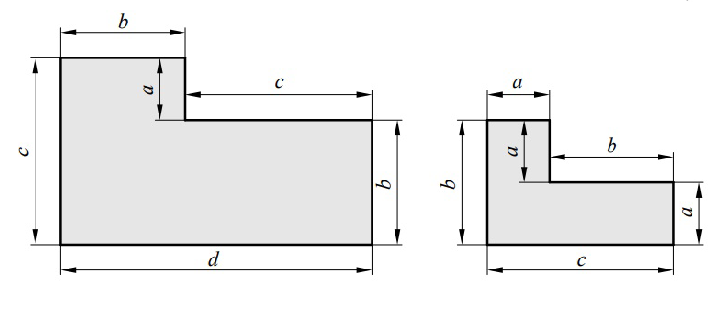
Nivel 1 Problema 12
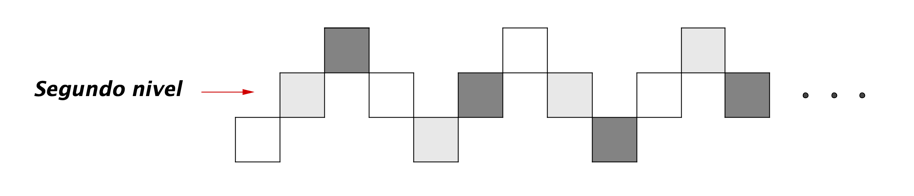
Se acomodan cuadrados formando escalones como en la figura hasta tener $2020$ cuadrados acomodados.
Estos cuadrados se colorean intercalando los colores blanco, gris y negro. ¿Cuántos cuadrados del segundo nivel de los escalones se colorean de color gris?
Estos cuadrados se colorean intercalando los colores blanco, gris y negro. ¿Cuántos cuadrados del segundo nivel de los escalones se colorean de color gris?
Nivel 1 Problema 13
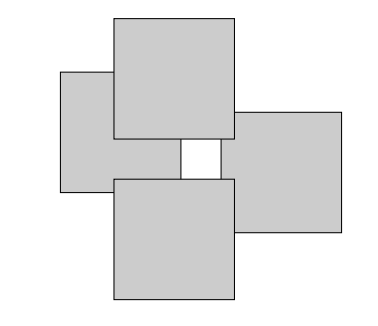
La siguiente figura se formó traslapando (encimando) cuadrados de área $81cm^2$ cada uno, y el cuadrado que se forma en el centro tiene área $9cm^2$. Si el cuadrado de arriba está exactamente arriba del cuadrado de abajo, es decir los lados verticales de los dos cuadrados están alineados, ¿cuánto vale el área sombreada?
Nivel 1 Problema 14
Considera todos los enteros positivos de la forma
\[1, 12, 123, \dots, 1234567891011, \dots\]
que resultan de escribir consecutivamente los primeros enteros. De los números anteriores, ¿cuántos dígitos tiene el número más pequeño donde aparece la cadena de números $2022$?
Nivel 1 Problema 15
Un gusano deberá recorrer todos los segmentos de la siguiente cuadrícula. Si recorre un segmento cada día, ¿cuál es el menor número de días que necesita el gusano para recorrer la cuadrícula?
Nota. El gusano puede recorrer $2$ o más veces un segmento, y no da saltos.
Nota. El gusano puede recorrer $2$ o más veces un segmento, y no da saltos.

Nivel 1 Equipos 1
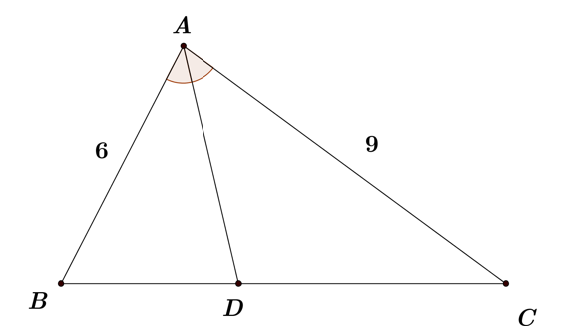
Sean $ABC$ un triángulo con $AB = 6$, $AC = 9$ y $D$ un punto del segmento $BC$ tal que $AD$ es bisectriz del ángulo $\angle A$. Si el área del triángulo $ABD$ es igual a $8$, ¿cuál es el área del triángulo $ABC$?
Nivel 1 Equipos 2
Ana y Eva juegan alternadamente a colocar fichas en las casillas de una cuadrícula de $9 \times 9$, con las tres reglas siguientes:
- en cada casilla vacía se coloca una sola ficha,
- en un turno pueden colocar 1, 2 o 3 fichas,
- perderá la que coloca la última ficha.
Nivel 1 Equipos 3
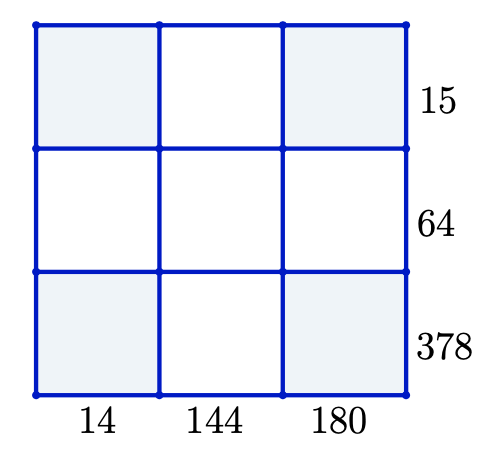
Los números enteros del 1 al 9 se escriben en los cuadros de la siguiente cuadrícula, uno en cada cuadro sin repetir. Los números que están a la derecha de cada fila son el producto de los dígitos escritos en la fila. Los números que están abajo de cada columna son el producto de los dígitos escritos en la columna. Encuentra el valor de la suma de los números escritos en los cuadros de las esquinas de la cuadrícula.
Nivel 1 Equipos 4
¿Cuántos números de tres dígitos $abc$ (con $a \neq 0$), tienen la propiedad de que los números de dos dígitos $ab$ y $bc$ son números primos?
Nivel 1 Equipos 5
Un número entero se dice que es ocholate si cumple las siguientes condiciones:
- Todos sus dígitos aparecen en orden creciente.
- Es múltiplo de 8 De los números ocholates de cuatro cifras, ¿cuál es la diferencia entre el mayor y el doble del menor de ellos?
Nivel 1 Equipos 6
Usando solo los vértices de un cubo se pueden formar 56 triángulos, ¿cuántos de estos triángulos son escalenos, es decir con sus tres lados de longitudes diferentes?
Nivel 1 Equipos 7
¿Cuántos números hay en la colección: $1, 2, 3, \dots, 2019, 2020$ que tengan al menos un dígito igual a 2 o un dígito igual a 0?
Nivel 1 Equipos 8
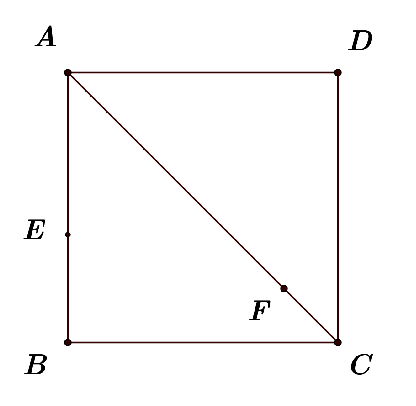
Sean $ABCD$ un cuadrado con medida de sus lados igual a $5cm$, $E$ un punto en el lado $AB$ con $AE = 3 cm$ y $F$ un punto en la diagonal $AC$ con $AF = 4FC$. Encuentra,
- El valor del área, en $cm^2$, del triángulo $DEF$.
- Las medidas de los ángulos, en grados, del triángulo $DEF$.
Nivel 2 Problema 1
Juan nació después del año $1970$ pero antes del $2000$. Si en el año $n^2$ Juan cumple $n$ años, ¿cuántos años cumple Juan en el año $2020$?
Nivel 2 Problema 2
Un píxel está formado por $3$ leds: uno rojo, uno verde y uno azul, donde cada uno puede prender con $4$ intensidades de luminosidad diferentes (además de que pueden estar apagados). Cada configuración de estos tres leds determina el color del píxel. ¿Cuántas configuraciones hay con el led azul prendido?
Nivel 2 Problema 3
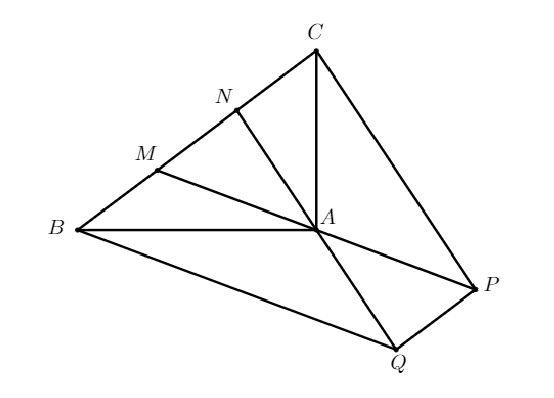
Sea $ABC$ un triángulo rectángulo con $\angle BAC = 90^\circ$ y área $12cm^2$. Sean $M$ y $N$ puntos en la hipotenusa $BC$ tales que $BM = MN = NC$. Se prolongan los segmentos $MA$ y $NA$ más allá de $A$, hasta los puntos $P$ y $Q$ tales que $MA = AP$ y $NA = AQ$. Encontrar el valor del área del cuadrilátero $BCPQ$ en $cm^2$.
Nivel 2 Problema 4
Una máquina A es capaz de cortar una determinada área de césped en $120$ minutos. Una máquina B corta esa misma área en $240$ minutos. Si se ponen a trabajar las dos máquinas al mismo tiempo para cortar esa área, ¿en cuántos minutos estará cortado el césped?
Nivel 2 Problema 5
En cada casilla de una cuadrícula de $3 \times 3$ hay una moneda. ¿De cuántas maneras se pueden quitar dos monedas que no se encuentren en casillas que comparten un lado?
Nivel 2 Problema 6
Cada número de $3$ cifras decimales se divide entre la suma de sus $3$ cifras y da un resultado. Por ejemplo, el número $207$ se divide entre $2+0+7=9$ dando como resultado $\frac{207}{9}=23$. ¿Cuál es el mayor valor que se puede obtener como resultado, al considerar todos los números de tres cifras?
Nivel 2 Problema 7
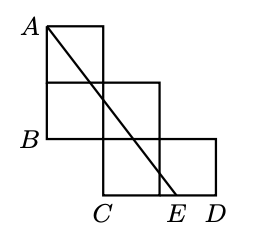
La siguiente figura está formada por $5$ cuadrados iguales de área $36 cm^2$ cada uno. Los puntos $A, B, C$ y $D$ son vértices de cuadrados. El punto $E$ del segmento $CD$ es tal que el segmento $AE$ divide a los $5$ cuadrados en dos partes de la misma área. Determinar la medida, en $cm$, del segmento $CE$.
Nivel 2 Problema 8
¿Cuántos números de la lista $1, 2, 3, \dots , 2019, 2020$ tienen al menos un dígito igual a $2$ o $0$?
Nivel 2 Problema 9
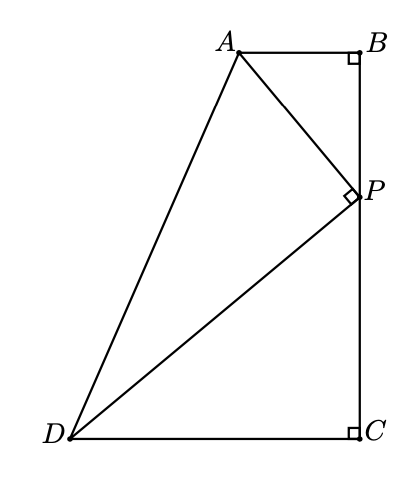
En la siguiente figura se tiene $AB = 5 cm$, $BC = 16 cm$ y $DC = 12 cm$. Si $BP \lt PC$, ¿cuánto mide, en $cm^2$, el área del triángulo $APD$?
Nivel 2 Problema 10
Se consideran todos los enteros positivos que se construyen escribiendo consecutivamente los primeros números enteros positivos. Por ejemplo, el que aparece en el primer lugar es el $1$, en segundo lugar aparece $12$, en el lugar $3$ aparece $123$, y así sucesivamente (en el lugar $12$ aparece $123456789101112$). De los números anteriores, ¿cuántos dígitos tiene el número más pequeño en el que aparece la cadena $2022$? Por ejemplo, el número de dígitos del número más pequeño en el que aparece la cadena $91$ es $11$ pues aparece por primera vez en el décimo número $12345678910$, el cual tiene $11$ dígitos.
Nivel 2 Problema 11
¿Cuántos subconjuntos de $3$ elementos (distintos) del conjunto $X = \{1, 2, 3, \dots , 20\}$ cumplen que el producto de los $3$ números del subconjunto es divisible entre $4$? Nota: Los subconjuntos $\{1, 2, 3\}, \{1, 3, 2\}$ y $\{2, 3, 1\}$ se consideran iguales.
Nivel 2 Problema 12
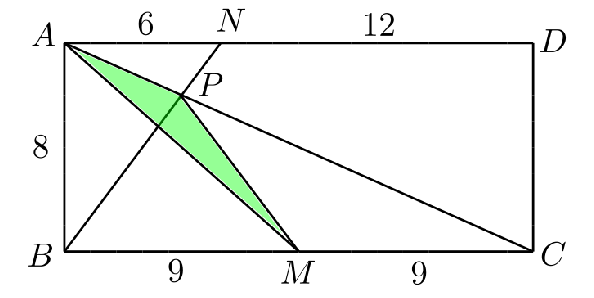
En la figura se muestra un rectángulo $ABCD$ con $AB = 8 cm$ y $BC = 18 cm$; $M$ es el punto medio de $BC$, $N$ es el punto del segmento $AD$ tal que $AN = 6 cm$, y $P$ es el punto de intersección de $AC$ con $BN$. Determinar el área, en $cm^2$, del triángulo $APM$.
Nivel 2 Problema 13
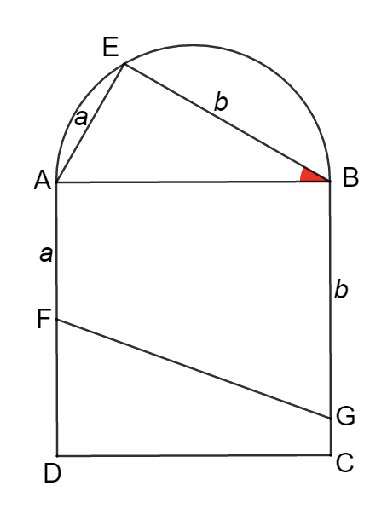
Sea $ABCD$ un cuadrado. Se dibuja, por fuera del cuadrado, un semicírculo que tenga al lado $AB$ como diámetro. Se escoge un punto $E$ en la semicircunferencia. Sean $G$ y $F$ puntos de los segmentos $BC$ y $AD$, respectivamente, tales que $GB=BE$ y $AF=AE$. Sean $a=AF$ y $b=GB$. Si las áreas entre $ABGF$ y $FGCD$ están a razón $a+b$, ¿cuánto mide el ángulo $\angle EBA$?
Nivel 2 Problema 14
Sea $x_0 = a$ con $a$ un número entero positivo. Para cada entero $n \gt 0$ definimos $x_n = 5x_{n-1} + 1$. ¿Cuántos valores de $a$ menores o iguales que $2020$ satisfacen que $x_k$ no es divisible entre $9$ para todo entero $k \geq 0$?
Nivel 2 Problema 15
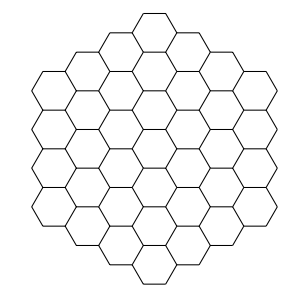
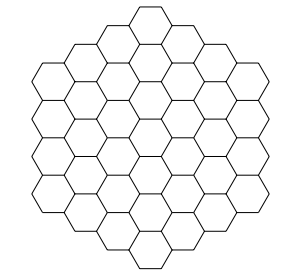
En la figura de abajo se muestra un panal de abejas. Dos hexágonos son vecinos si comparten una arista. Si en cada hexágono cabe a lo más una abeja, ¿cuál es la mayor cantidad de abejas que pueden vivir en dicho panal de modo que no haya abejas vecinas?
Nivel 2 Equipos 1
Determinar la cantidad de números enteros que son múltiplos de 3 y tienen 5 dígitos distintos escogidos dentro de la lista $1, 2, 3, 4, 5, 6, 7$ pero dos de sus dígitos son 1 y 2, en ese orden. Por ejemplo, 31725 y 31254 son números de los que queremos, mientras que 32715 y 31724 no.
Nivel 2 Equipos 2
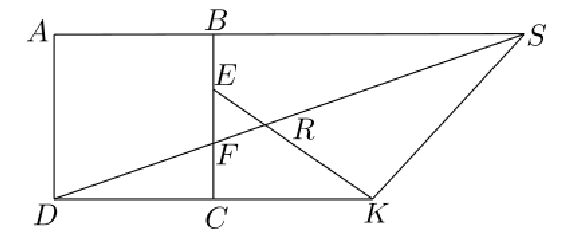
En la figura se muestra un cuadrado $ABCD$ de área $36 cm^2$. Los puntos $E$ y $F$ sobre $BC$ son tales que $BE = EF = FC$; el punto $K$ sobre la recta $CD$ es tal que $C$ es el punto medio del segmento $DK$. La recta $DF$ intersecta a las rectas $EK$ y $AB$ en $R$ y $S$, respectivamente. Determinar el área, en $cm^2$, del triángulo $KRS$.
Nivel 2 Equipos 3
¿Cuántos números de tres dígitos, $abc$ (con $a \neq 0$), tienen la propiedad de que los números de dos dígitos $ab$ y $bc$ son números primos? Por ejemplo, un número que cumple es 237 pues tanto 23 como 37 son primos.
Nivel 2 Equipos 4
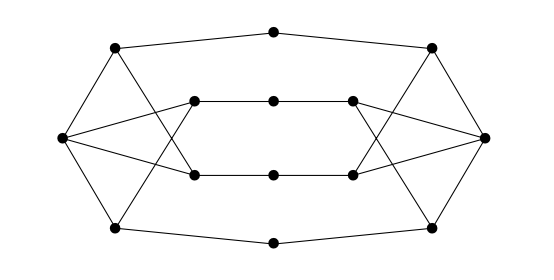
La siguiente figura consta de 14 vértices y 20 segmentos. Se dice que dos vértices son vecinos si hay una línea que empieza en uno de ellos y acaba en otro. Raúl quiere elegir algunos vértices de manera que entre los vértices que eligió y sus vecinos, estén elegidos todos los vértices. ¿Cuál es la mínima cantidad de vértices que debe elegir Raúl para lograr esto?
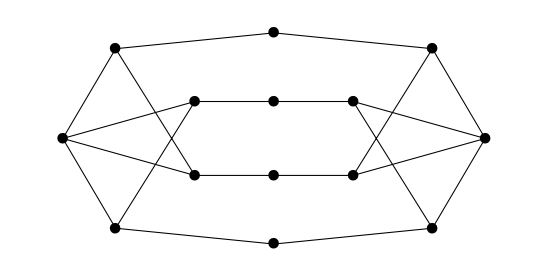
Nivel 2 Equipos 5
Una ficha sombrero es una como la que se muestra en la figura, donde cada cuadrito es de $1 \times 1$. Se quiere cubrir una cuadrícula de $6 \times 40$ con fichas sombrero, de tal manera que las fichas no se traslapen, no se salgan del tablero y los lados de las fichas sean paralelos a los lados de la cuadrícula. ¿De cuántas formas distintas puede llenarse el tablero, considerando que las fichas pueden rotarse?

Nivel 2 Equipos 6
Encontrar la suma de todos los números enteros $n$ de tres dígitos distintos, para los cuales la suma de todos los números de dos dígitos que se pueden formar con los dígitos de $n$ sea igual al doble de $n$. Por ejemplo, si $n = 123$, entonces los números de dos dígitos distintos que se pueden formar con los dígitos de $n$ son 12, 13, 21, 23, 31 y 32.
Nivel 2 Equipos 7
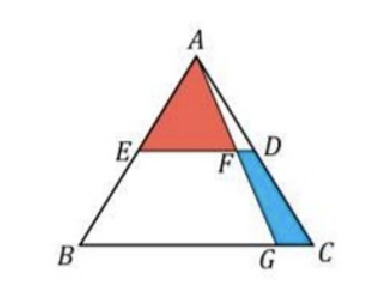
En la figura, $ABC$ es un triángulo equilátero cuyos lados miden $28 cm$. Los puntos medios de $AB$ y $AC$ son $E$ y $D$, respectivamente. ¿Cuál debe ser el valor de la longitud del segmento $BG$, en $cm$, para que el área del triángulo $AEF$ sea igual al doble del área del cuadrilátero $CDFG$?
Nivel 2 Equipos 8
En un país, se tienen ciudades que inician con cada letra del abecedario (el cual cuenta con 26 letras). Hay una ciudad cuyo nombre empieza con la letra $a$, dos ciudades cuyos nombres empiezan con la letra $b$, tres ciudades con la letra $c$, cuatro ciudades con $d$ y así sucesivamente. Solo se puede pasar de una ciudad a otra si las letras con las que empieza su nombre son vecinas en el abecedario; por ejemplo, $c$ es vecino de $b$ y $d$, así como $a$ es vecino de $b$ y $z$. ¿Se pueden recorrer todas las ciudades sin repetir?
Nivel 3 Problema 1
En cada casilla de una cuadrícula de $3 \times 3$ hay una moneda. ¿De cuántas maneras se pueden quitar dos monedas que no se encuentren en casillas que comparten un lado?
Nivel 3 Problema 2
Sean $a$, $b$ y $c$ enteros positivos diferentes tales que su suma y su producto son cuadrados perfectos. Determina el menor valor posible de $abc(a + b + c)$.
Nivel 3 Problema 3
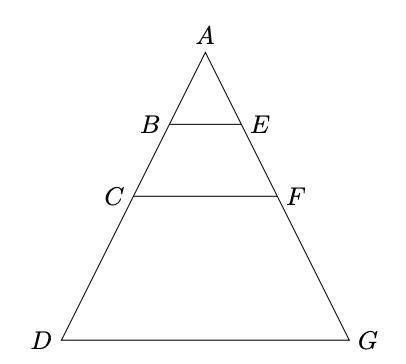
En la siguiente figura se sabe que la altura del triángulo $ABE$ es la mitad de la altura del triángulo $ACF$, y a su vez la altura del triángulo $ACF$ es la mitad de la altura del triángulo $ADG$. Si el perímetro del triángulo $ABE$ es $7cm$ y el perímetro del trapecio $CDGF$ es $22cm$, ¿cuál es el perímetro, en centímetros, del trapecio $BDGE$?
Nivel 3 Problema 4
¿Cuántos subconjuntos de tres elementos (distintos) se pueden escoger del conjunto $\{1,2,3,\dots,19,20\}$ de manera que el producto de los tres números no sea divisible entre $4$?
Nivel 3 Problema 5
La lista $1, x_2, x_3, \dots , x_n, 200$ es la sucesión más larga de enteros positivos tal que cada término a partir del tercero es la suma de los anteriores, es decir,
\[x_3=1+x_2, x_4=1+x_2+x_3, x_5=1+x_2+x_3+x_4\]
y así sucesivamente. Determina el valor de $x_2$.
Nivel 3 Problema 6
Los números reales distintos $a,b,c,d$ satisfacen que $a+c = b+d$ y $a+b+cd = c+d+ab$. Determina la suma de los posibles valores de $a + c$.
Nivel 3 Problema 7
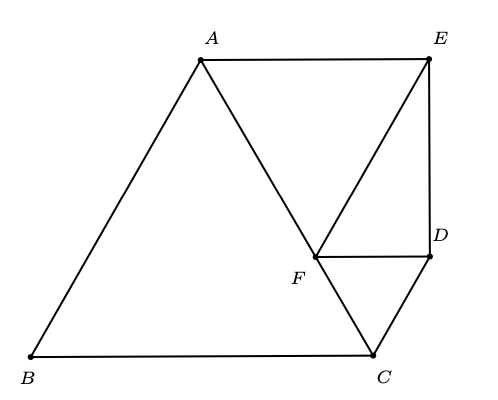
Sean $ABC$, $AFE$ y $CDF$ triángulos equiláteros como se muestra en la figura cuyas medidas de sus lados son $6 cm$, $4 cm$ y $2 cm$, respectivamente. Si el área del pentágono ABCDE es $x cm^2$, encuentra el valor de $x^2$.
Nivel 3 Problema 8
En la figura de abajo se muestra un panal de abejas. Dos hexágonos son vecinos si comparten una arista. Si en cada hexágono cabe a lo más una abeja, ¿cuál es la mayor cantidad de abejas que pueden vivir en dicho panal de modo que no haya abejas vecinas?
Nivel 3 Problema 9
Sea $x_0 = a$ con $a$ un número entero positivo. Para cada entero $n \gt 0$ definimos $x_n = 5x_{n-1} + 1$. ¿Cuántos valores de $a$ menores o iguales que $2020$ satisfacen que $x_k$ no es divisible entre $9$ para todo entero $k \geq 0$?
Nivel 3 Problema 10
Sea $f(x) = x^2 + 3x + 2$. Si el producto
\[\left(1-\frac{2}{f(1)}\right)\left(1-\frac{2}{f(2)}\right)\left(1-\frac{2}{f(3)}\right)\dots\left(1-\frac{2}{f(100)}\right)\]
puede escribirse como $\frac ab$ donde $a$ y $b$ son enteros positivos primos relativos, encuentra el valor de $a+b$.
Nivel 3 Problema 11
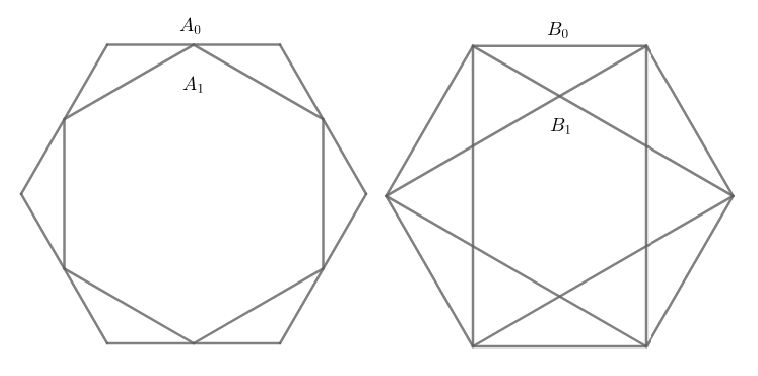
Los hexágonos regulares $A_0$ y $B_0$ tienen lados iguales a $1$. Para cada entero positivo $n$, el hexágono regular $A_n$ se construye uniendo los puntos medios de los lados del hexágono regular $A_{n-1}$. El hexágono regular $B_n$ se construye traslapando dos triángulos equiláteros con vértices de $B_{n-1}$. En la siguiente figura se muestran los hexágonos regulares $A_1$ y $B_1$. La razón del área de $A_{2020}$ entre el área de $B_{2020}$ puede escribirse de la forma $(\frac ab)^c$ donde $a,b,c$ son enteros positivos y $a$, $b$ son primos relativos. Si $c$ toma el valor máximo posible, encuentra el valor de $\frac{c}{a+b}$ .
Nivel 3 Problema 12
El número de mi casa tiene cuatro dígitos diferentes. Si se suman todos los números que se pueden formar con tres de esos cuatro dígitos, se obtiene un total igual al cuadrado de la suma de esos cuatro dígitos multiplicado por mi edad e igual al número de mi casa multiplicado por $\frac{36}{13}$. Encuentra el cociente del número de mi casa entre mi edad.
Nivel 3 Problema 13
Sean $ABC$ y $ADE$ dos triángulos isósceles semejantes entre sí, donde $AB = AC$, $AD = AE$ y $\angle BAD = \angle CAE$. Llamemos $M$, $N$ y $F$ a los puntos medios de $BC$, $DE$ y $BE$, respectivamente. Determina el valor de la razón $\frac{MF}{FN}$.
Nivel 3 Problema 14
Determina todos los enteros $a$, $b$ y $c$ distintos de cero tales que $a$ sea divisor de $b - c$, $b$ sea divisor de $c - a$ y $c$ sea divisor de $a - b$.
Nivel 3 Problema 15
En un $2n$-ágono regular se han marcado sus vértices, sus lados, su centro y las $n$ diagonales que pasan por el centro. Si $A$ y $B$ son dos vértices diametralmente opuestos del $2n$-ágono, ¿de cuántas formas se puede ir de $A$ a $B$ moviéndose sobre las líneas de la figura sin pasar dos veces por el mismo punto?
Nivel 3 Equipos 1
Daniela está parada en el vértice $A$ del cuadrado $ABCD$. Va a lanzar una moneda: si cae águila, avanzará al siguiente vértice en el sentido de las manecillas del reloj; si cae sol, avanzará al vértice anterior en el sentido de las manecillas del reloj. Si Daniela lanza la moneda un total de 10 veces y tras el último lanzamiento Daniela cae en el vértice $A$, ¿de cuántas formas pudo haber sucedido esto?
Nivel 3 Equipos 2
La siguiente figura consta de 14 vértices y 20 segmentos. Se dice que dos vértices son vecinos si hay una línea que empieza en uno de ellos y acaba en otro. Raúl quiere elegir algunos vértices de manera que entre los vértices que eligió y sus vecinos, estén elegidos todos los vértices. ¿Cuál es la mínima cantidad de vértices que debe elegir Raúl para lograr esto?
Nivel 3 Equipos 3
Encontrar la suma de todos los números enteros $n$ de tres dígitos distintos, para los cuales la suma de todos los números de dos dígitos que se pueden formar con los dígitos de $n$ sea igual al doble de $n$. Por ejemplo, si $n = 123$, entonces los números de dos dígitos distintos que se pueden formar con los dígitos de $n$ son 12, 13, 21, 23, 31 y 32.
Nivel 3 Equipos 4
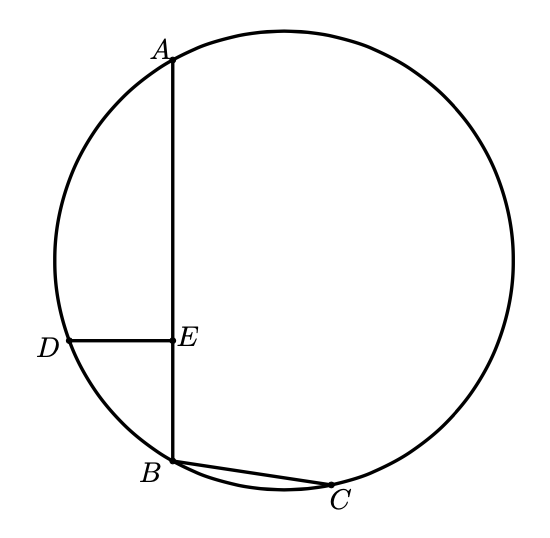
En la siguiente figura, los puntos $A$, $D$, $B$ y $C$ están sobre una misma circunferencia $\Gamma$. El punto $E$ está sobre el segmento $AB$ de tal manera que $DE$ es perpendicular a $AB$. Si $EB = 3 cm$, $BC = 4 cm$ y $AD = DC$, encuentra la medida, en $cm$, del segmento $AE$.
Nivel 3 Equipos 5
Emmanuel tiene un candado con una clave de 4 dígitos, pero se le olvidó la contraseña. Recuerda que todos los dígitos son diferentes, que el número es múltiplo de 45, que tiene exactamente un dígito par y que el número comienza con 9 o 4. Si $k$ es el mínimo número de intentos que requiere para poder asegurar que sabe la clave del candado, ¿cuál es el valor de 100$k$?
Nivel 3 Equipos 6
Sean a, b y c números reales que cumplen,
\[a^2-ab=b^2-bc=c^2-ca=1.\]
Determina el valor numérico de $abc(a + b + c)$.
Nivel 3 Equipos 7
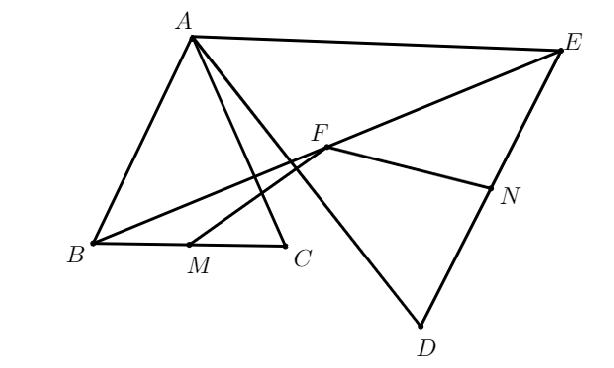
En el cuadrilátero convexo $ABCD$, se tiene que $\angle BAD + \angle ABC = 120^\circ$, $AD = BC = 5 cm$ y $AB = 8 cm$. Además, se construye por fuera del cuadrilátero el triángulo equilátero $CDE$. Si el área del triángulo $ABE$ es de $x cm^2$, encuentra el valor de $x^2$.
Nivel 3 Equipos 8
Demuestra que si $n$ es un entero positivo tal que $3n + 1$ y $10n + 1$ son cuadrados, entonces $29n + 11$ no puede ser un número primo.