OMMEB

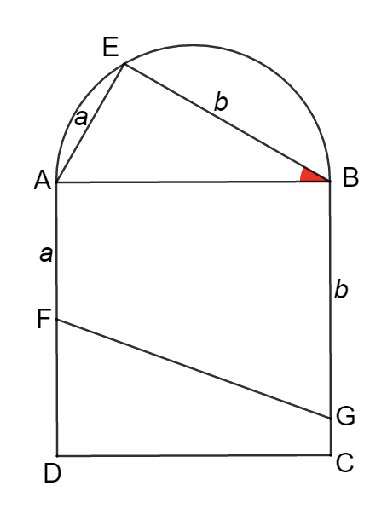
Sea $ABCD$ un cuadrado. Se dibuja, por fuera del cuadrado, un semicírculo que tenga al lado $AB$ como diámetro. Se escoge un punto $E$ en la semicircunferencia. Sean $G$ y $F$ puntos de los segmentos $BC$ y $AD$, respectivamente, tales que $GB=BE$ y $AF=AE$. Sean $a=AF$ y $b=GB$. Si las áreas entre $ABGF$ y $FGCD$ están a razón $a+b$, ¿cuánto mide el ángulo $\angle EBA$?

Descargar Imagen